

【探究】 本題可以用兩種方法來證明,一是作平面的垂線而后證明它在另一個平面內(證法一);二是在一個平面內找一條線段,證明它與另一個平面垂直(證法二).
證法一:作AD⊥平面BSC,D為垂足.
∵∠ASB=∠ASC=60°,SA=SB=SC,則AS=AB=AC,
∴D為△BSC的外心.又∠BSC=90°,
∴D為BC的中點,即AD在平面ABC內.
∴平面ABC⊥平面BSC.
證法二:取BC的中點D,連結AD、SD,易證AD⊥BC.又△ABS是正三角形,△BSC為等腰直角三角形,∴BD=SD.∴AD2+SD2=AD2+BD2=AB2=AS2.
由勾股定理的逆定理,知AD⊥SD,∴AD⊥平面BSC.
又AD![]() 平面ABC,∴平面ABC⊥平面BSC.
平面ABC,∴平面ABC⊥平面BSC.
【規律總結】 本題是證明面面垂直的典型例題,關鍵是將證明“面面垂直”的問題轉化為證明“線面垂直”的問題.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源:2013年高考數學備考復習卷8:立體幾何(解析版) 題型:解答題
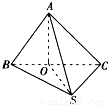 如圖,過S引三條長度相等但不共面的線段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求證:平面ABC⊥平面BSC.
如圖,過S引三條長度相等但不共面的線段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求證:平面ABC⊥平面BSC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com