已知數列{a
n}的各項均為正數,其前n項和為S
n,且
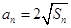
-1,
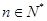
,數列
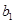
,
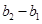
,
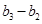
……,
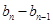
是首項為1,公比為
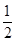
的等比數列。
(I)求證:數列{a
n}是等差數列;
(II)若
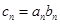
,求數列{c
n}的前n項和Tn。
解(Ⅰ)∵
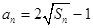
,
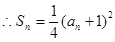
當
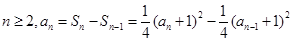
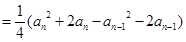
即
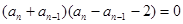
,
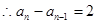
又
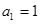
故數列
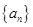
是等差數列.且
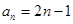
; ………4分
(Ⅱ)∵
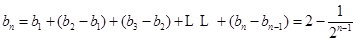
………6分
∴
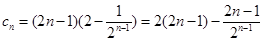
………7分
先求數列
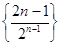
的前
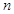
項和
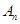
.
∵
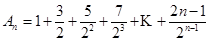
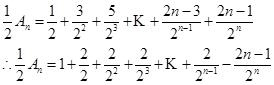
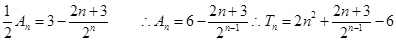
.
………12分
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)在數列
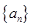
中,
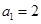
,
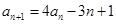
,
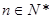
.
(Ⅰ)證明數列
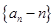
是等比數列;
(Ⅱ)求數列
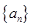
的前
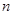
項和
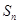
;
(Ⅲ)令
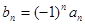
,求數列
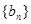
的前
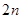
項和
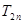
。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
對于數列
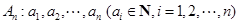
,定義“

變換”:

將數列
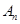
變換成數列
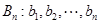
,其中
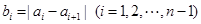
,且
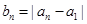
,這種“

變換”記作
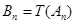
.繼續對數列
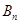
進行“

變換”,得到數列
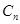
,…,依此類推,當得到的數列各項均為
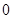
時變換結束.
(Ⅰ)試問
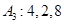
和
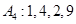
經過不斷的“

變換”能否結束?若能,請依次寫出經過“

變換”得到的各數列;若不能,說明理由;
(Ⅱ)求
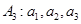
經過有限次“

變換”后能夠結束的充要條件;
(Ⅲ)證明:
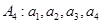
一定能經過有限次“

變換”后結束.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列{b
n}是等差數列, b
1="1," b
1+b
2+b
3+…+b
10=100.
(Ⅰ)求數列{b
n}的通項公式;
(Ⅱ)設數列{a
n}的通項
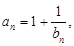
記T
n是數列{a
n}的前n項之積,即T
n= b
1·b
2·b
3…b
n,試證明:
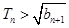
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
觀察下列等式:
1=1 1
3=1
1+2=3 1
3+2
3=9
1+2+3=6 1
3+2
3+3
3=36
1+2+3+4=10 1
3+2
3+3
3+4
3=100
1+2+3+4+5=15 1
3+2
3+3
3+4
3+5
3=225
……
可以推測:1
3+2
3+3
3+…+n
3=
。(
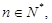
用含有n的代數式表示)
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
若
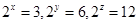
,則x,y,z三個數依次成什么數列
| A.成等差數列,但不成等比數列; | B.成等比數列 ,但不成等差數列; |
| C.既是等差數列,又是等比數列; | D.既不是等差數列,也不是等比數列; |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
等差數列{an}中,已知
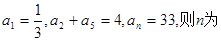
( )
查看答案和解析>>
主站蜘蛛池模板:
久久精品一区二区三区不卡牛牛
|
狠狠色综合网站久久久久久久
|
国产一区二区精品在线观看
|
亚洲 欧美 另类 综合 偷拍
|
精品视频免费在线
|
91精品国产综合久久久蜜臀粉嫩
|
成人精品在线视频
|
亚洲精品乱码久久久久久金桔影视
|
欧美一区不卡
|
国产精品视频专区
|
日本电影黄色
|
精品久久一区二区
|
一级在线
|
欧美成人a∨高清免费观看
久久精品在线
|
成人免费的视频
|
精品久久久久久久久久久久久久久
|
伊人网在线免费观看
|
精品影视
|
国产亚洲一区二区三区在线
|
在线播放亚洲
|
亚洲国产福利
|
成人黄色91|
视频一区二
|
欧美精品福利视频
|
啪啪小视频网站
|
黄色片av
|
久久久夜
|
精品亚洲成a人片在线观看
99在线免费视频
|
久久久久久免费视频
|
精产国产伦理一二三区
|
亚洲成人一区二区
|
99精品久久久久
|
日韩精品免费观看
|
天天综合7799精品影视
|
日韩欧美中文在线
|
亚洲精品v日韩精品
|
日韩在线免费电影
|
国产不卡视频在线观看
|
蜜桃视频一区二区三区
|
四虎永久在线
|
欧美日韩无
|

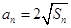 -1,
-1,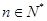 ,數列
,數列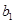 ,
,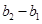 ,
,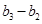 ……,
……,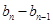 是首項為1,公比為
是首項為1,公比為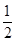 的等比數列。
的等比數列。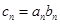 ,求數列{cn}的前n項和Tn。
,求數列{cn}的前n項和Tn。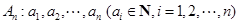 ,定義“
,定義“ 變換”:
變換”: 將數列
將數列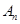 變換成數列
變換成數列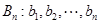 ,其中
,其中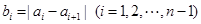 ,且
,且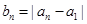 ,這種“
,這種“ 變換”記作
變換”記作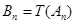 .繼續對數列
.繼續對數列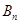 進行“
進行“ 變換”,得到數列
變換”,得到數列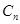 ,…,依此類推,當得到的數列各項均為
,…,依此類推,當得到的數列各項均為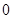 時變換結束.
時變換結束.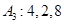 和
和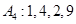 經過不斷的“
經過不斷的“ 變換”能否結束?若能,請依次寫出經過“
變換”能否結束?若能,請依次寫出經過“ 變換”得到的各數列;若不能,說明理由;
變換”得到的各數列;若不能,說明理由;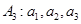 經過有限次“
經過有限次“ 變換”后能夠結束的充要條件;
變換”后能夠結束的充要條件;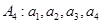 一定能經過有限次“
一定能經過有限次“ 變換”后結束.
變換”后結束.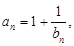 記Tn是數列{an}的前n項之積,即Tn= b1·b 2·b 3…bn,試證明:
記Tn是數列{an}的前n項之積,即Tn= b1·b 2·b 3…bn,試證明: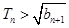
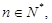 用含有n的代數式表示)
用含有n的代數式表示)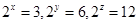 ,則x,y,z三個數依次成什么數列
,則x,y,z三個數依次成什么數列