
已知拋物線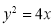 ,直線
,直線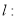
 與拋物線交于
與拋物線交于 兩點.
兩點.
(Ⅰ)若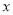 軸與以
軸與以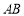 為直徑的圓相切,求該圓的方程;
為直徑的圓相切,求該圓的方程;
(Ⅱ)若直線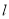 與
與 軸負半軸相交,求
軸負半軸相交,求 面積的最大值.
面積的最大值.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)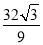 .
.
【解析】
試題分析:(Ⅰ)聯立 ,消
,消 并化簡整理得
并化簡整理得 ,利用圓與
,利用圓與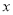 軸相切的位置關系得弦
軸相切的位置關系得弦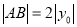 從而確定
從而確定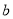 的值,進而求得該圓的方程;
的值,進而求得該圓的方程;
(Ⅱ)首先根據直線與拋物線的位置關系將弦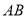 的長度和原點到直線
的長度和原點到直線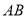 的距離均表示為
的距離均表示為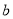 的函數,并確定
的函數,并確定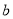 的取值范圍,從而把
的取值范圍,從而把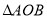 的面積也表示為
的面積也表示為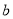 的函數,最后利用函數的最值求出
的函數,最后利用函數的最值求出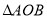 的最大值.
的最大值.
試題解析:(Ⅰ)聯立 ,消
,消 并化簡整理得
并化簡整理得 .
.
依題意應有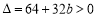 ,解得
,解得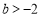 .
.
設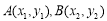 ,則
,則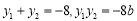 ,
,
設圓心 ,則應有
,則應有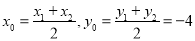 .
.
因為以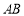 為直徑的圓與
為直徑的圓與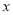 軸相切,得到圓半徑為
軸相切,得到圓半徑為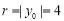 ,
,
又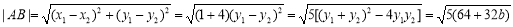 .
.
所以 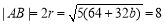 ,
,
解得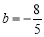 .
.
所以 ,所以圓心為
,所以圓心為 .
.
故所求圓的方程為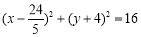 .
.
(Ⅱ)因為直線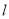 與
與 軸負半軸相交,所以
軸負半軸相交,所以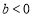 ,
,
又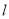 與拋物線交于兩點,由(Ⅱ)知
與拋物線交于兩點,由(Ⅱ)知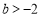 ,所以
,所以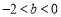 ,
,
直線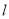 :
: 整理得
整理得 ,點
,點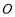 到直線
到直線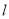 的距離
的距離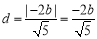 ,
,
所以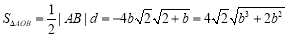 . 令
. 令 ,
,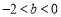 ,
,
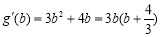 ,
,
|
|
|
|
| + | 0 | - |
|
| 極大 |
|
由上表可得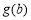 的最大值為
的最大值為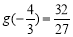 .所以當
.所以當 時,
時,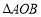 的面積取得最大值
的面積取得最大值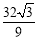 .
.
考點:1、直線與拋物線的位置關系;導數在研究函數性質中的應用.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源:2014-2015學年山東省日照市高三12月校際聯合檢測理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)某風景區在一個直徑AB為100米的半圓形花園中設計一條觀光線路(如圖所示).在點A與圓弧上的一點C之間設計為直線段小路,在路的兩側邊緣種植綠化帶;從點C到點B設計為沿弧BC的弧形小路,在路的一側邊緣種植綠化帶.(注:小路及綠化帶的寬度忽略不計)

(1)設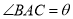 (弧度),將綠化帶總長度表示為
(弧度),將綠化帶總長度表示為 的函數
的函數 ;
;
(2)試確定 的值,使得綠化帶總長度最大.
的值,使得綠化帶總長度最大.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年河北省等五校高三上學期第二次聯考文科數學試卷(解析版) 題型:選擇題
下列函數最小正周期為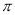 且圖象關于直線
且圖象關于直線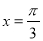 對稱的函數是
對稱的函數是
A.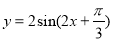 B.
B.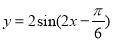
C.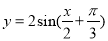 D.
D.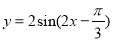
查看答案和解析>>
科目:高中數學 來源:2014-2015學年河北省等五校高三上學期第二次聯考理科數學試卷(解析版) 題型:填空題
設點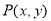 滿足條件
滿足條件 ,點
,點 滿足
滿足 恒成立,其中
恒成立,其中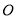 是坐標原點,則
是坐標原點,則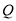 點的軌跡所圍成圖形的面積是 .
點的軌跡所圍成圖形的面積是 .
查看答案和解析>>
科目:高中數學 來源:2014-2015學年河北省等五校高三上學期第二次聯考理科數學試卷(解析版) 題型:選擇題
等差數列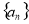 的前
的前 項和為
項和為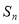 ,且
,且 ,
,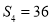 ,則過點
,則過點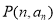 和
和 (
(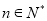 )的直線的一個方向向量是( )
)的直線的一個方向向量是( )
A.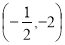 B.
B.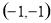 C.
C. 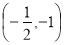 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com