
已知函數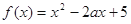 (
(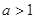 ).
).
(1)若 的定義域和值域均是
的定義域和值域均是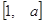 ,求實數
,求實數 的值;
的值;
(2)若對任意的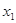 ,
,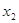
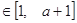 ,總有
,總有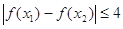 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1)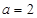 ;(2)
;(2)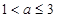
解析試題分析:(1)求出二次函數的對稱軸是關鍵.通過對稱軸知道函數f(x)在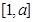 上單調遞減.在結合已知條件即可得兩個等式.求出結論.
上單調遞減.在結合已知條件即可得兩個等式.求出結論.
(2)條件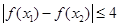 表示的含義是函數f(x)在
表示的含義是函數f(x)在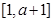 上的最大值與最小值的差小于或等于4.因為函數f(x)的對稱軸為
上的最大值與最小值的差小于或等于4.因為函數f(x)的對稱軸為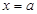 .所以要將
.所以要將 的值分兩類
的值分兩類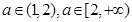 .再根據單調性即可求得
.再根據單調性即可求得 的范圍.本題的函數的背景是二次函數所以抓住對稱軸展開研究函數的最值單調性.同時分類的思想是解題的關鍵.
的范圍.本題的函數的背景是二次函數所以抓住對稱軸展開研究函數的最值單調性.同時分類的思想是解題的關鍵.
試題解析:(1)因為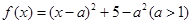 .所以f(x)在
.所以f(x)在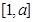 是減函數,又定義域和值域為
是減函數,又定義域和值域為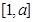 所以
所以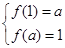 .即
.即 .解得
.解得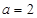 .
.
(2)若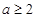 .又
.又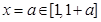 ,且
,且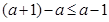 .所以
.所以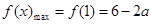 .
.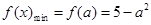 .因為對任意的
.因為對任意的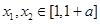 .總有
.總有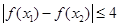 .所以
.所以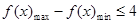 .即
.即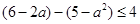 .解得
.解得 .又
.又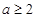 .所以
.所以 .若
.若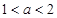 .
.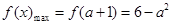 .
.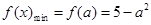 .
.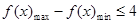 顯然成立.綜上
顯然成立.綜上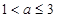 .
.
考點:1.二次函數的對成性.2.函數的最值問題.3.分類思想想.


科目:高中數學 來源: 題型:解答題
某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為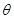 (弧度).
(弧度).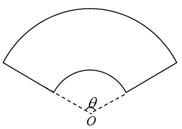
(1)求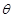 關于
關于 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為 ,求
,求 關于
關于 的函數關系式,并求出
的函數關系式,并求出 為何值時,
為何值時, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如果函數 滿足在集合
滿足在集合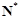 上的值域仍是集合
上的值域仍是集合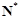 ,則把函數
,則把函數 稱為N函數.
稱為N函數.
例如: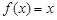 就是N函數.
就是N函數.
(Ⅰ)判斷下列函數:①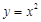 ,②
,②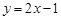 ,③
,③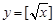 中,哪些是N函數?(只需寫出判斷結果);
中,哪些是N函數?(只需寫出判斷結果);
(Ⅱ)判斷函數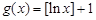 是否為N函數,并證明你的結論;
是否為N函數,并證明你的結論;
(Ⅲ)證明:對于任意實數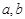 ,函數
,函數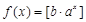 都不是N函數.
都不是N函數.
(注:“ ”表示不超過
”表示不超過 的最大整數)
的最大整數)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某自來水廠的蓄水池存有400噸水,水廠每小時可向蓄水池中注水60噸,同時蓄水池又向居民小區不間斷供水,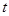 小時內供水總量為
小時內供水總量為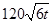 噸(
噸(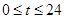 ),從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
),從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經市場調查,某種商品在過去50天的銷售量和價格均為銷售時間t(天)的函數,且銷售量近似地滿足f(t)=-2t+200(1≤t≤50,t∈N).前30天價格為g(t)=t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
(1)寫出該種商品的日銷售額S與時間t的函數關系;
(2)求日銷售額S的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com