

 時,求函數
時,求函數 的最大值;
的最大值; (
( )其圖象上任意一點
)其圖象上任意一點 處切線的斜率
處切線的斜率 ≤
≤ 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍; ,
, ,方程
,方程 有唯一實數解,求正數
有唯一實數解,求正數 的值.
的值. ;(2)
;(2) ; (3)
; (3)
 的取值范圍;(3)構建函數模型,利用函數的增減性,分析出方程有唯一解,即函數有唯一零點的情況,從而得出正數m的值.
的取值范圍;(3)構建函數模型,利用函數的增減性,分析出方程有唯一解,即函數有唯一零點的情況,從而得出正數m的值. ,
,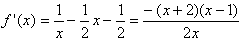 ,
,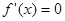 , 解得x=1,(∵x>0),
, 解得x=1,(∵x>0), 時,
時,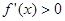 ,此時f(x)單調遞增,
,此時f(x)單調遞增, ,此時f(x)單調遞減,
,此時f(x)單調遞減, ,此即為最大值.
,此即為最大值. ,則有
,則有 上恒成立,
上恒成立, ,當
,當 取得最大值
取得最大值 ,所以
,所以 .
. 有唯一實數解,所以
有唯一實數解,所以 有唯一實數解,
有唯一實數解, ,則
,則 ,令
,令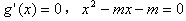 ,
, ,
, 上單調遞減;
上單調遞減; 上單調遞增;
上單調遞增; ,
, ,所以
,所以 ,
,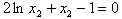 ,(*)
,(*) ,因為當x>0時,h(x)是增函數,所以h(x)=0至多有一解,
,因為當x>0時,h(x)是增函數,所以h(x)=0至多有一解, ,即
,即 ,解得
,解得 .
.

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com