
【題目】已知函數![]() (
(![]() ).
).
(1)若函數![]() 是單調函數,求
是單調函數,求![]() 的取值范圍;
的取值范圍;
(2)求證:當![]() 時,都有
時,都有![]() .
.
【答案】(1)![]() 或
或![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)對函數求導,由函數![]() 是單調函數可得
是單調函數可得![]() 或
或![]() 在
在![]() 上恒成立,利用分離參數的方法,當
上恒成立,利用分離參數的方法,當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,分別求右端的最值或極限值即可;(2)由(1)可知,當
,分別求右端的最值或極限值即可;(2)由(1)可知,當![]() 時,
時, ![]() 在
在![]() 上遞減,根據單調性化簡可得
上遞減,根據單調性化簡可得![]() 成立,利用分析法將所證命題轉化為
成立,利用分析法將所證命題轉化為![]() ,構造函數
,構造函數![]() ,求出
,求出![]() 即可.
即可.
試題解析:(1)函數![]() 的定義域為
的定義域為![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵函數![]() 是單調函數,∴
是單調函數,∴![]() 或
或![]() 在
在![]() 上恒成立,
上恒成立,
①∵![]() ,∴
,∴![]() ,即
,即![]() ,
, ![]() ,
,
令![]() ,則
,則![]() ,當
,當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
則![]() 在
在![]() 上遞減,
上遞減, ![]() 上遞增,∴
上遞增,∴![]() ,∴
,∴![]() ;
;
②∵![]() ,∴
,∴![]() ,即
,即![]() ,
, ![]() ,
,
由①得![]() 在
在![]() 上遞減,
上遞減, ![]() 上遞增,又
上遞增,又![]() ,
, ![]() 時
時![]() ,∴
,∴![]() ;綜上①②可知,
;綜上①②可知, ![]() 或
或![]() ;
;
(2)由(1)可知,當![]() 時,
時, ![]() 在
在![]() 上遞減,∵
上遞減,∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
要證![]() ,只需證
,只需證![]() ,即證
,即證![]() ,
,
令![]() ,
, ![]() ,則證
,則證![]() ,令
,令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上遞減,又
上遞減,又![]() ,∴
,∴![]() ,即
,即![]() ,得證.
,得證.


科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面積為10
,△ABC的面積為10 ![]() ,求BC邊上的中線長.
,求BC邊上的中線長. 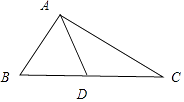
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ].
].
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)設函數f(x)= ![]()
![]() ,求f(x)的最大值及單調遞增區間.
,求f(x)的最大值及單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我省城鄉居民社會養老保險個人年繳費分100,200,300,400,500,600,700,800,900,1000(單位:元)十個檔次,某社區隨機抽取了50名村民,按繳費在100:500元,600:1000元,以及年齡在20:39歲,40:59歲之間進行了統計,相關數據如下:
100﹣500元 | 600﹣1000 | 總計 | |
20﹣39 | 10 | 6 | 16 |
40﹣59 | 15 | 19 | 34 |
總計 | 25 | 25 | 50 |
(1)用分層抽樣的方法在繳費100:500元之間的村民中隨機抽取5人,則年齡在20:39歲之間應抽取幾人?
(2)在繳費100:500元之間抽取的5人中,隨機選取2人進行到戶走訪,求這2人的年齡都在40:59歲之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛);
轎車A | 轎車B | 轎車C | |
舒適型 | 100 | 150 | z |
標準型 | 300 | 450 | 600 |
按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有A類轎車10輛.
(1)求z的值;
(2)用分層抽樣的方法在C類轎車中抽取一個容量為5的樣本,將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
(3)用隨機抽樣的方法從B類舒適型轎車中抽取8輛,經檢測它們的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把這8輛轎車的得分看成一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值不超過0.5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側棱
中,側棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() .
.
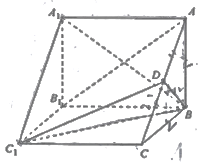
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,側面PAD⊥底面ABCD,E,F分別為PA,BD中點,PA=PD=AD=2.
(Ⅰ)求證:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一點G,使GF⊥平面EDF?若存在,指出點G的位置;若不存在,說明理由.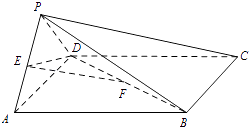
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com