Question

在一張矩形的紙張上畫一幅宣傳畫，紙張的上、下邊緣各留8厘米空白，左右邊緣各留5厘米空白，其余的地方用來作畫，要求畫面面積為4840平方厘米．
（1）設畫面的高為x厘米，紙張面積為y平方厘米，寫出y關于x的函數解析式．
（2）怎樣確定畫面的高與寬的尺寸，能使宣傳畫所用紙張面積最小？

Answer 1

解：（1）根據畫面高為xcm，紙張面積為y平方厘米，則有
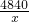
y=（x+16）（+10）=+10x+5000，（x＞0）
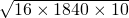
（2）由于x＞0，得+10x≥2+5000=1760
當=10x，即x=88 時，y取得最小值，
答：當畫面的高為88cm，寬為55cm時能使所用的紙張面積最小．
分析：（1）根據畫面高為xcm，紙張面積為y平方厘米，根據矩形的面積公式建立面積的表達式；
（2）根據（1）中的解析式，然后根據基本不等求出函數的最值即可．
點評：本題主要考查了函數模型的選擇與應用，以及基本不等式在最值問題中的應用，屬于中檔題．