
 )+mlnx+
)+mlnx+ (m∈R,x>0),
(m∈R,x>0),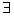 x>0使f(x)≤0成立,求實數m的取值范圍;
x>0使f(x)≤0成立,求實數m的取值范圍; x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1.
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1. 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:高中數學 來源:四川省平武中學2011屆高三一診模擬演練理科數學試題 題型:044
已知二次函數g(x)的圖象經過坐標原點,且滿足g(x+1)=g(x)+2x+1.設函數f(x)=mg(x)-ln(x+1),其中m為非零常數.
(1)求函數g(x)的解析式;
(2)當-2<m<0時,判斷函數f(x)的單調性并且說明理由;
(3)證明:對任意的正整數n,不等式ln(![]() +1)>
+1)>![]() -
-![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中數學 來源:江蘇省無錫市洛社中學2012屆高三上學期12月月考數學試題 題型:044
已知二次函數g(x)對任意實數x都滿足g(x)=g(1-x),g(x)的最小值為-![]() 且g(1)=-1.令f(x)=g(x+
且g(1)=-1.令f(x)=g(x+![]() )+mlnx+
)+mlnx+![]() (m∈R,x>0).
(m∈R,x>0).
(1)求g(x)的表達式;
(2)若![]() x>0使f(x)≤0成立,求實數m的取值范圍;
x>0使f(x)≤0成立,求實數m的取值范圍;
(3)設1<m≤e,H(x)=f(x)-(m+1)x,證明:對![]() x1、x2∈[1,m],恒有|H(x1)-H(x2)|<1.
x1、x2∈[1,m],恒有|H(x1)-H(x2)|<1.
查看答案和解析>>
科目:高中數學 來源:江蘇模擬題 題型:解答題
 )+mlnx+
)+mlnx+ (m∈R),
(m∈R),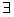 x>0使f(x)≤0成立,求實數m的取值范圍;
x>0使f(x)≤0成立,求實數m的取值范圍;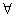 x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。
x1,x2∈[1,m],恒有|H(x1)-H(x2)|<1。 查看答案和解析>>
科目:高中數學 來源:湖南省模擬題 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com