
【題目】某中學調查了某班全部![]() 名同學參加學校社團的情況,數據如下表:(單位:人)
名同學參加學校社團的情況,數據如下表:(單位:人)
參加書法社 | 未參加書法社 | |
參加辯論社 |
|
|
未參加辯論社 |
|
|
(1)從該班隨機選![]() 名同學,求該同學至少參加一個社團的概率;
名同學,求該同學至少參加一個社團的概率;
(2)在既參加書法社又參加辯論社的![]() 名同學中,有
名同學中,有![]() 名男同學
名男同學![]() ,
,![]() 名女同學
名女同學![]() .現從這
.現從這![]() 名同學中男女姓各隨機選
名同學中男女姓各隨機選![]() 人(每人被選到的可能性相同).
人(每人被選到的可能性相同).
(i)列舉出所有可能結果;
(ii)設![]() 為事件“
為事件“![]() 被選中且
被選中且![]() 未被選中”,求事件
未被選中”,求事件![]() 發生的概率.
發生的概率.
科目:高中數學 來源: 題型:
【題目】高鐵是我國國家名片之一,高鐵的修建凝聚著中國人的智慧與汗水.如圖所示,B、E、F為山腳兩側共線的三點,在山頂A處測得這三點的俯角分別為![]() 、
、![]() 、
、![]() ,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.
,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.
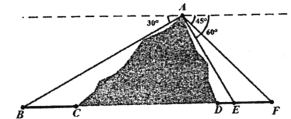
(1)求出線段AE的長度;
(2)求出隧道CD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義![]() 上的函數
上的函數![]() ,若滿足:對任意
,若滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界.
的上界.
(1)設![]() ,判斷
,判斷![]() 在
在![]() 上是否有界函數,若是,請說明理由,并寫出
上是否有界函數,若是,請說明理由,并寫出![]() 的所有上界的值的集合,若不是,也請說明理由;
的所有上界的值的集合,若不是,也請說明理由;
(2)若函數![]() 在
在![]() 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,當P(x,y)不是原點時,定義P的“伴隨點”為![]() ;
;
當P是原點時,定義P的“伴隨點“為它自身,平面曲線C上所有點的“伴隨點”所構成的曲線![]() 定義為曲線C的“伴隨曲線”.現有下列命題:
定義為曲線C的“伴隨曲線”.現有下列命題:
①若點A的“伴隨點”是點![]() ,則點
,則點![]() 的“伴隨點”是點A
的“伴隨點”是點A
②單位圓的“伴隨曲線”是它自身;
③若曲線C關于x軸對稱,則其“伴隨曲線”![]() 關于y軸對稱;
關于y軸對稱;
④一條直線的“伴隨曲線”是一條直線.
其中的真命題是_____________(寫出所有真命題的序列).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】王先生購買了一部手機,欲使用中國移動“神州行”卡或加入聯通的![]() 網,經調查其收費標準見下表:(注:本地電話費以分為計費單位,長途話費以秒為計費單位.)
網,經調查其收費標準見下表:(注:本地電話費以分為計費單位,長途話費以秒為計費單位.)
網絡 | 月租費 | 本地話費 | 長途話費 |
甲:聯通 |
|
|
|
乙:移動“神州行” | 無 |
|
|
若王先生每月撥打本地電話的時間是撥打長途電話時間的![]() 倍,若要用聯通
倍,若要用聯通![]() 應最少打多長時間的長途電話才合算.( )
應最少打多長時間的長途電話才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,函數
,函數![]() .
.
(1)設![]() ,
,![]() ,若
,若![]() 是奇函數,求
是奇函數,求![]() 的值;
的值;
(2)設![]() ,
,![]() ,判斷函數
,判斷函數![]() 在
在![]() 上的單調性并加以證明;
上的單調性并加以證明;
(3)設![]() ,
,![]() ,
,![]() ,函數
,函數![]() 的圖象是否關于某垂直于
的圖象是否關于某垂直于![]() 軸的直線對稱?如果是,求出該對稱軸,如果不是,請說明理由.
軸的直線對稱?如果是,求出該對稱軸,如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() 是滿足下列性質的函數
是滿足下列性質的函數![]() 的全體,存在實數
的全體,存在實數![]()
![]() ,對于定義域內的任意
,對于定義域內的任意![]() 均有
均有![]() 成立,稱數對
成立,稱數對![]() 為函數
為函數![]() 的“伴隨數對”.
的“伴隨數對”.
(1)判斷![]() 是否屬于集合
是否屬于集合![]() ,并說明理由;
,并說明理由;
(2)若函數![]() ,求滿足條件的函數
,求滿足條件的函數![]() 的所有“伴隨數對”;
的所有“伴隨數對”;
(3)若![]() ,
,![]() 都是函數
都是函數![]() 的“伴隨數對”,當
的“伴隨數對”,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .求當
.求當![]() 時,函數
時,函數![]() 的零點.
的零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且點
,且點![]()
![]() 在函數
在函數![]() 的圖像上;
的圖像上;
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足:
滿足:![]() ,
,![]() ,求
,求![]() 的通項公式;
的通項公式;
(3)在第(2)問的條件下,若對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com