
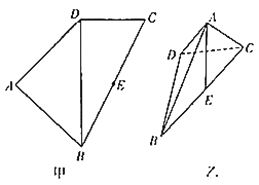
【題目】如圖甲,四邊形![]() 中,
中,![]() 是
是![]() 的中點,
的中點, ![]() .將(圖甲)沿直線
.將(圖甲)沿直線![]() 折起,使二面角
折起,使二面角![]() 為
為![]() (如圖乙).
(如圖乙).
(1)求證:![]() ⊥平面
⊥平面![]()
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,可知
,可知![]() ,
,![]() 平面
平面![]() ,即
,即![]() ,也可證明
,也可證明![]() ,根據線面垂直的判斷定理可證
,根據線面垂直的判斷定理可證![]() 平面
平面![]() ;(2)根據等體積轉化
;(2)根據等體積轉化![]() ,可得點到平面的距離,或是利用空間直角坐標解決.
,可得點到平面的距離,或是利用空間直角坐標解決.
試題解析:(Ⅰ)證明:如圖,取BD中點M,連接AM,ME.
![]()
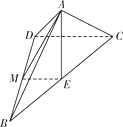
因為AB=AD=![]() ,所以AM⊥BD, 因為DB=2,DC=1,BC=
,所以AM⊥BD, 因為DB=2,DC=1,BC=![]() ,滿足:DB 2+DC 2=BC 2, 所以△BCD是以BC為斜邊的直角三角形,BD⊥DC,因為E是BC的中點,所以ME為△BCD的中位線,
,滿足:DB 2+DC 2=BC 2, 所以△BCD是以BC為斜邊的直角三角形,BD⊥DC,因為E是BC的中點,所以ME為△BCD的中位線,![]() ME∥
ME∥![]() ,
,![]() ME⊥BD,ME=
ME⊥BD,ME=![]()
![]() ∠AME是二面角A-BD-C的平面角,
∠AME是二面角A-BD-C的平面角,![]() =
=![]() °.
°.
![]() ,
,![]() 且AM、ME是平面AME內兩條相交于點M的直線,
且AM、ME是平面AME內兩條相交于點M的直線,
![]() ,
,![]() 平面AEM,
平面AEM,![]() .
.
![]() ,
,![]() ,
,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,在△AME中,由余弦定理得:
,在△AME中,由余弦定理得:
![]()
![]()
![]() ,
,![]() .
.
(Ⅱ)解法一:等體積法.
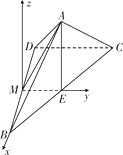
解法二:如圖5,以M為原點,MB所在直線為x軸,ME所在直線為y軸,
平行于EA的直線為z軸,建立空間直角坐標系,
則由(Ⅰ)及已知條件可知B(1,0,0),![]() ,
,![]() ,D
,D![]() ,C
,C![]() .則
.則![]()
![]() 設平面ACD的法向量為
設平面ACD的法向量為![]() =
=![]() ,
,
則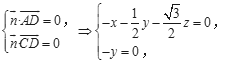 令
令![]() 則z=-2,
則z=-2,![]()
![]() 到平面
到平面![]() 的距離為d,則
的距離為d,則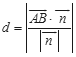 ,所以d
,所以d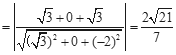 .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知P點到兩定點D(﹣2,0),E(2,0)連線斜率之積為- ![]() .
.
(1)求證:動點P恒在一個定橢圓C上運動;
(2)過 ![]() 的直線交橢圓C于A,B兩點,過O的直線交橢圓C于M,N兩點,若直線AB與直線MN斜率之和為零,求證:直線AM與直線BN斜率之和為定值.
的直線交橢圓C于A,B兩點,過O的直線交橢圓C于M,N兩點,若直線AB與直線MN斜率之和為零,求證:直線AM與直線BN斜率之和為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有關于x的一元二次方程x2+2ax+b2=0.
(1)若a是從0,1,2,3四個數中任取的一個數,b是從0,1,2三個數中任取的一個數,求上述方程有實根的概率.
(2)若a是從區間[0,3]任取的一個數,b是從區間[0,2]任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC為等邊三角形,AE=1,BD=2,CD與平面ABCDE所成角的正弦值為 ![]() .
. 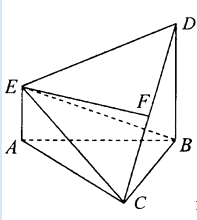
(1)若F是線段CD的中點,證明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2x,g(x)是一次函數,并且點(2,2)在函數f[(g(x)]的圖象上,點(2,5)在函數g[f(x)]的圖象上,則g(x)的解析式為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示為某幾何體形狀的紙盒的三視圖,在此紙盒內放一個小正四面體,若小正四面體在紙盒內可以任意轉動,則小正四面體的棱長的最大值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品的保鮮時間t(單位:小時)與儲藏溫度x(單位:℃)滿足函數關系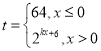 且該食品在4℃的保鮮時間是16小時.
且該食品在4℃的保鮮時間是16小時.
已知甲在某日上午10時購買了該食品,并將其遺放在室外,且此日的室外溫度隨時間變化如圖所示.給出以下四個結論:

①該食品在6℃的保鮮時間是8小時;
②當x∈[﹣6,6]時,該食品的保鮮時間t隨著x增大而逐漸減少;
③到了此日13時,甲所購買的食品還在保鮮時間內;
④到了此日14時,甲所購買的食品已然過了保鮮時間.
其中,所有正確結論的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com