
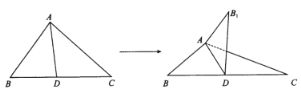
【題目】如圖,已知![]() 中,
中,![]() 是
是![]() 的平分線,將
的平分線,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,在翻折過程中,設所成二面角
,在翻折過程中,設所成二面角![]() 的平面角為
的平面角為![]() ,
,![]() ,則下列結(jié)論中成立的是( )
,則下列結(jié)論中成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
過B點作![]() 的垂線,分別交
的垂線,分別交![]() 于點M,N,連接
于點M,N,連接![]() ,由二面角的平面角的定義,知
,由二面角的平面角的定義,知![]() ,根據(jù)
,根據(jù)![]() 為
為![]() 的平分線,得到
的平分線,得到![]() ,由
,由![]() ,得到
,得到![]() 的關(guān)系,再通過余弦定理,
的關(guān)系,再通過余弦定理,![]() ,
,![]() ,結(jié)合
,結(jié)合![]() ,得到
,得到![]() 關(guān)系即可.
關(guān)系即可.
解法一:過B點作![]() 的垂線,分別交
的垂線,分別交![]() 于點M,N,連接
于點M,N,連接![]() ,如圖.
,如圖.

由二面角的平面角的定義,知![]() .
.
又![]() 為
為![]() 的平分線,則
的平分線,則![]() .
.
在共底邊的等腰![]() 與等腰
與等腰![]() 中,
中,![]() ,
,
故![]() .
.
又由余弦定理,有![]() ,
,
同理:![]() ,
,
因為![]() 且
且![]() ,
,
則![]() ,即
,即![]() ,
,
故選:B
解法二:過B點作![]() 的垂線,分別交
的垂線,分別交![]() 于點M,N,本題可以考慮
于點M,N,本題可以考慮![]() 的兩個特殊位置:
的兩個特殊位置:
(1)![]() 翻折時初始位置,此時二面角
翻折時初始位置,此時二面角![]() 的平面角
的平面角![]() 與
與![]() 均為平角,
均為平角,![]() ,故
,故![]() ;
;
(2)![]() 翻轉(zhuǎn)180°時,
翻轉(zhuǎn)180°時,![]() 與
與![]() 與
與![]() 分別重合,則
分別重合,則![]() .
.
綜合即得![]() ,
,
故選:B.


科目:高中數(shù)學 來源: 題型:
【題目】已知正△ABC邊長為3,點M,N分別是AB,AC邊上的點,AN=BM=1,如圖1所示.將△AMN沿MN折起到△PMN的位置,使線段PC長為![]() ,連接PB,如圖2所示.
,連接PB,如圖2所示.
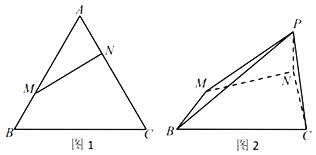
(Ⅰ)求證:平面PMN⊥平面BCNM;
(Ⅱ)若點D在線段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() ,已知函數(shù)
,已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)求函數(shù)![]() 在
在![]() 上的最小值
上的最小值![]() ;
;
(Ⅲ)若![]() , 求使方程
, 求使方程![]() 有唯一解的
有唯一解的![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設點M是棱長為2的正方體ABCD-A1B1C1D1的棱AD的中點,點P在面BCC1B1所在的平面內(nèi),若平面D1PM分別與平面ABCD和平面BCC1B1所成的銳二面角相等,則點P到點C1的最短距離是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() ,
,![]() ,是自然對數(shù)的底數(shù).
,是自然對數(shù)的底數(shù).
(1)若曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,求
,求![]() 的值;
的值;
(2)求函數(shù)![]() 的極大值;
的極大值;
(3)設函數(shù)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學”的口號,鼓勵學生線上學習.某校數(shù)學教師為了調(diào)查高三學生數(shù)學成績與線上學習時間之間的相關(guān)關(guān)系,對高三年級隨機選取45名學生進行跟蹤問卷,其中每周線上學習數(shù)學時間不少于5小時的有19人,余下的人中,在檢測考試中數(shù)學平均成績不少于120分的有10人,統(tǒng)計成績后得到如下![]() 列聯(lián)表:
列聯(lián)表:
分數(shù)不少于120分 | 分數(shù)不足120分 | 合計 | |
線上學習時間不少于5小時 | 4 | 19 | |
線上學習時間不足5小時 | 10 | ||
合計 | 45 |
(1)請完成上面![]() 列聯(lián)表;并判斷是否有99%的把握認為“高三學生的數(shù)學成績與學生線上學習時間有關(guān)”;
列聯(lián)表;并判斷是否有99%的把握認為“高三學生的數(shù)學成績與學生線上學習時間有關(guān)”;
(2)在上述樣本中從分數(shù)不少于120分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于5小時和線上學習時間不足5小時的學生共5名,若在這5名學生中隨機抽取2人,求至少1人每周線上學習時間不足5小時的概率.
(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式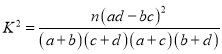 其中
其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C:![]() 1(a>b>0),F1,F2為橢圓的左右焦點,過F2的直線交橢圓與A、B兩點,∠AF1B=90°,2
1(a>b>0),F1,F2為橢圓的左右焦點,過F2的直線交橢圓與A、B兩點,∠AF1B=90°,2![]() ,則橢圓的離心率為( )
,則橢圓的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
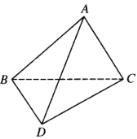
【題目】如圖,![]() 是以
是以![]() 為斜邊的等腰直角三角形,
為斜邊的等腰直角三角形,![]() 中
中![]() ,
,![]() 沿著
沿著![]() 翻折成三棱錐
翻折成三棱錐![]() 的過程中,直線
的過程中,直線![]() 與平面
與平面![]() 所成的角均小于直線
所成的角均小于直線![]() 與平面
與平面![]() 所成的角,設二面角
所成的角,設二面角![]() ,
,![]() 的大小分別為
的大小分別為![]() ,
,![]() ,則( ).
,則( ).
A.![]() B.
B.![]()
C.存在![]() D.
D.![]() ,
,![]() 的大小關(guān)系不能確定
的大小關(guān)系不能確定
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com