【題目】解不等式： 
≥2．
【答案】解：不等式移項得： 
﹣2≥0， 變形得： 
≤0，
即2（x﹣ 
）（x﹣6）（x﹣3）（x﹣5）≤0，且x≠3，x≠5，
根據題意畫出圖形，如圖所示：
根據圖形得： ≤x＜3或5＜x≤6，
則原不等式的解集為[ ，3）∪（5，6]．
【解析】把不等式的右邊移項到左邊，通分后把分子分母都分解因式，得到的式子小于等于0，然后根據題意畫出圖形，在數軸上即可得到原不等式的解集．
【考點精析】根據題目的已知條件，利用解一元二次不等式的相關知識可以得到問題的答案，需要掌握求一元二次不等式
解集的步驟：一化：化二次項前的系數為正數;二判：判斷對應方程的根;三求：求對應方程的根;四畫：畫出對應函數的圖象;五解集：根據圖象寫出不等式的解集;規律：當二次項系數為正時，小于取中間，大于取兩邊．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知在平面直角坐標系
中， 
為坐標原點，曲線
： 
（
為參數），在以平面直角坐標系的原點為極點， 
軸的正半軸為極軸，有相同單位長度的極坐標系中，直線
： 
.
(Ⅰ)求曲線
的普通方程和直線
的直角坐標方程；
(Ⅱ)求與直線
平行且與曲線
相切的直線的直角坐標方程。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知 
=（ 
sinx，m+cosx）， 
=（cosx，﹣m+cosx），且f（x）= 
（1）求函數f（x）的解析式；
（2）當x∈ 
時，f（x）的最小值是﹣4，求此時函數f（x）的最大值，并求出相應的x的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解甲、乙兩個工廠生產的輪胎的寬度是否達標，分別從兩廠隨機各選取了10個輪胎，將每個輪胎的寬度（單位：mm）記錄下來并繪制出如下的折線圖：
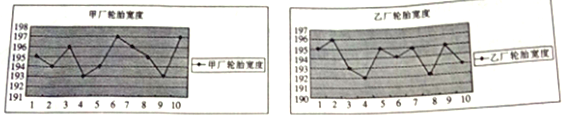
（1）分別計算甲、乙兩廠提供的10個輪胎寬度的平均值；
（2）輪胎的寬度在
內，則稱這個輪胎是標準輪胎.試比較甲、乙兩廠分別提供的10個輪胎中所有標準輪胎寬度的方差的大小，根據兩廠的標準輪胎寬度的平均水平及其波動情況，判斷這兩個工廠哪個廠的輪胎相對更好？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】原命題：“
， 
為兩個實數，若
，則
， 
中至少有一個不小于1”，下列說法錯誤的是（ ）
A. 逆命題為：若
， 
中至少有一個不小于1，則
，為假命題
B. 否命題為：若
，則
， 
都小于1，為假命題
C. 逆否命題為：若
， 
都小于1，則
，為真命題
D. “
”是“
， 
中至少有一個不小于1”的必要不充分條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為調查高一新生上學路程所需要的時間（單位：分鐘），從高一年級新生中隨機抽取100名新生按上學所需時間分組：第1組（0，10]，第2組（10，20]，第3組（20，30]，第4組（30，40]，第5組（40，50]，得到的頻率分布直方圖如圖所示．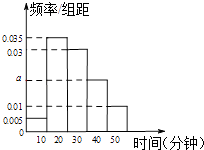
（1）根據圖中數據求a的值；
（2）若從第3，4，5組中用分層抽樣的方法抽取6名新生參與交通安全問卷調查，應從第3，4，5組各抽取多少名新生？
（3）在（2）的條件下，該校決定從這6名新生中隨機抽取2名新生參加交通安全宣傳活動，求第4組至少有一名志愿者被抽中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠為了對新研發的一種產品進行合理定價，將該產品按事先擬定的價格進行試銷，得到如下數據：
單價x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
（1）求回歸直線方程 
= 
x+ 
，其中 =﹣20， = 
﹣ 
（2）預計在今后的銷售中，銷量與單價仍然服從（1）中的關系，且該產品的成本是4元/件，為使工廠獲得最大利潤，該產品的單價應定為多少元？（利潤=銷售收入﹣成本）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
