【題目】已知函數(shù)
，求證：
（1）
在區(qū)間
存在唯一極大值點；
（2）在
上有且僅有2個零點.
【答案】（1）證明見解析（2）證明見解析
【解析】
（1）首先求出函數(shù)的導數(shù)
，設
，對
求導，說明其單調性，再根據(jù)零點存在性定理可得在
有唯一零點，從而得證；
（2）結合（1）的單調性利用零點存在性定理證明
上有兩個零點，當
時無零點.
解：（1）因為
，所以
，
設，則
，則當
時，
，
所以即在單調遞減，
又
，
，且圖像是不間斷的，
由零點存在性定理可得在有唯一零點，設為
.
則當
時，
；當
時，
.
所以
在
單調遞增，在
單調遞減，
故在存在唯一極大值點.
（2）因為，所以，
設，則，則當
時，，
所以即在單調遞減，
由（1）知，在單調遞增，在單調遞減.
又
，
，所以
，
又的圖像是不間斷的，所以存在
，使得
；
又當
時，
，所以在
遞減，
因
，又
，又的圖像是不間斷的，
所以存在
，使得
；
當時，
，
，所以
，從而在
沒有零點.
綜上，有且僅有2個零點.
同步輕松練習系列答案
課課通課程標準思維方法與能力訓練系列答案科目：高中數(shù)學 來源： 題型：
【題目】下列關于簡單幾何體的說法中正確的是（ ）
①有兩個面互相平行，其余各面都是平行四邊形的多面體是棱柱；
②有一個面是多邊形，其余各面都是三角形的幾何體是棱錐；
③有兩個底面平行且相似，其余各面都是梯形的多面體是棱臺；
④空間中到定點的距離等于定長的所有點的集合是球面．
A.①②B.③④C.④D.②④
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】圓周上有800個點，依順時針方向標號為
，它們將圓周分成800個間隙.今選定某一點染成紅色，然后按如下規(guī)則，逐次染紅其余的一些點：如果第
號點已被染紅，則可按順時針方向轉過個間隙，再將所到達的那個端點染紅.如此繼續(xù)下去.試問圓周上最多可得到多少個紅點？證明你的結論.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某大學餐飲中心為了解新生的飲食習慣，在全校一年級學生中進行了抽樣調查，調查結果如下表所示：
喜歡甜品 | 不喜歡甜品 | 合計 | |
南方學生 | 60 | 20 | 80 |
北方學生 | 10 | 10 | 20 |
合計 | 70 | 30 | 100 |
（1）根據(jù)表中數(shù)據(jù)，問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差異”；
（2）已知在被調查的北方學生中有5名數(shù)學系的學生，其中2名喜歡甜品.現(xiàn)在從這5名學生中隨機抽取3人，求至多有1人喜歡甜品的概率.
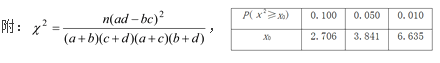
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知角α的頂點與原點O重合，始邊與x軸的非負半軸重合，它的終邊上有一點P的坐標是（3a，a），其中a≠0．
（1）求cos（α
）的值；
（2）若tan（2α+β）＝1，求tanβ的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】給定兩個七棱錐，它們有公共面的底面
，頂點
、
在底面的兩則.現(xiàn)將下述線段中的每一條染紅、藍兩色之一:
，底面上的所有對角線和所有的側棱.求證：圖中心存在一個同色三角形.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】邊長為1的菱形
的兩對角線交于
,過作A2B2∥A1B1交
于
連結
交
于
,過作A3B3∥A1B1交于
,…,這樣作下去得
以
為原點,所在直線為
軸,建立平面直角坐標系,設以
為半徑,圓心在
,軸上的一列圓
依次相外切(即
與
外切,
),若圓T1與拋物線
相切.求證:所有的圓都與拋物線相切.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
