
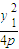 ,y1)、B(
,y1)、B(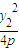 ,y2).OA⊥OB可得A、B的縱坐標之積、橫坐標之積均為定值,由OM⊥AB可知OM和AB斜率之積為-1,且M點在直線AB上,求出M點的軌跡方程;
,y2).OA⊥OB可得A、B的縱坐標之積、橫坐標之積均為定值,由OM⊥AB可知OM和AB斜率之積為-1,且M點在直線AB上,求出M點的軌跡方程;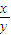 代入直線方程即可.
代入直線方程即可. ,kAB=-
,kAB=- ,
, (x-x)+y.
(x-x)+y.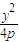 ,將其代入上式,整理,得
,將其代入上式,整理,得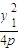 ,y1)、B(
,y1)、B(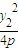 ,y2).
,y2).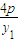 •
•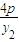 =-1.∴y1y2=-16p2.
=-1.∴y1y2=-16p2.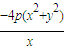 ,∴
,∴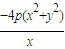 =16p2.
=16p2.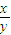 .
.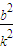 .消去x,得ky2-4py+4pb=0.所以y1y2=
.消去x,得ky2-4py+4pb=0.所以y1y2=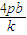 .由OA⊥OB,
.由OA⊥OB,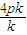 =-
=-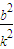 ,b=-4kp.
,b=-4kp. 代入,得
代入,得

科目:高中數學 來源:山東省莘縣實驗高中2011-2012學年高二下學期第一次月考數學理科試題 題型:013
已知拋物線y2=2px(p>0)的焦點弦AB的兩端點為A(x1,y1),B(x2,y2),則關系式![]() 的值一定等于
的值一定等于
A.4p
B.-4p
C.p2
D.-p
查看答案和解析>>
科目:高中數學 來源:湖南石門一中2007屆高三第二次月考理科數學試卷 題型:022
已知拋物線的方程為y2=4px(p>0),A為拋物線上的點,F為焦點,若|AF|=4p,則|OA|的值為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com