
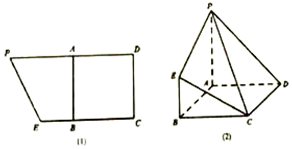
 已知梯形CEPD如圖(1)所示,其中PD=8,CE=6,A為線段PD的中點,四邊形ABCD為正方形,現沿AB進行折疊,使得平面PABE⊥平面ABCD,得到如圖(2)所示的幾何體.已知當點F滿足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)時,平面DEF⊥平面PCE,則λ的值為( )
已知梯形CEPD如圖(1)所示,其中PD=8,CE=6,A為線段PD的中點,四邊形ABCD為正方形,現沿AB進行折疊,使得平面PABE⊥平面ABCD,得到如圖(2)所示的幾何體.已知當點F滿足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)時,平面DEF⊥平面PCE,則λ的值為( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 以A為原點,AB為x軸,AD為y軸,AP為z軸,建立空間直角從標系,利用向量法能求出λ的值.
解答 解: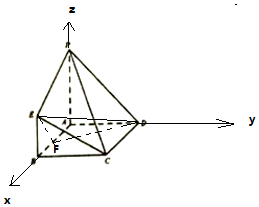 由題意,以A為原點,AB為x軸,AD為y軸,AP為z軸,建立空間直角坐標系,
由題意,以A為原點,AB為x軸,AD為y軸,AP為z軸,建立空間直角坐標系,
則D(0,4,0),E(4,0,2),C(4,4,0),P(0,0,4),A(0,0,0),B(4,0,0),
設F(t,0,0),0≤t≤4,$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1),
則(t,0,0)=(4λ,0,0),∴t=4λ,∴F(4λ,0,0),
$\overrightarrow{DE}$=(4,-4,2),$\overrightarrow{DF}$=(4λ,-4,0),$\overrightarrow{PC}$=(4,4,-4),$\overrightarrow{PE}$=(4,0,-2),
設平面DEF的法向量$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=4x-4y+2z=0}\\{\overrightarrow{n}•\overrightarrow{DF}=4λx-4y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,λ,2λ-2),
設平面PCE的法向量$\overrightarrow{m}$=(a,b,c),
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PC}=4a+4b-4c=0}\\{\overrightarrow{m}•\overrightarrow{PE}=4a-2c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,1,2),
∵平面DEF⊥平面PCE,
∴$\overrightarrow{n}•\overrightarrow{m}$=1+λ+2(2λ-2)=0,解得$λ=\frac{3}{5}$.
故選:C.
點評 本題考查實數值的求法,是基礎題,解題時要認真審題,注意向量法的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $4\sqrt{3\sqrt{2}}$ | B. | $5\sqrt{4\sqrt{3\sqrt{2}}}$ | C. | $5\sqrt{4}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
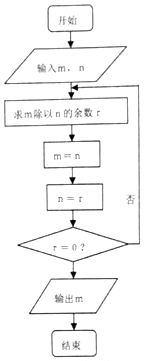 如圖程序框圖的算法思路源于歐幾里得名著《幾何原本》中的“輾轉相除法”,執行該程序框圖,若輸入m,n分別為225、135,則輸出的m=( )
如圖程序框圖的算法思路源于歐幾里得名著《幾何原本》中的“輾轉相除法”,執行該程序框圖,若輸入m,n分別為225、135,則輸出的m=( )| A. | 5 | B. | 9 | C. | 45 | D. | 90 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
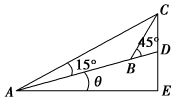 如圖所示,在坡度一定的山坡A處測得山頂上一建筑物CD的頂端C對于山坡的斜度為15°,向山頂前進100m到達B處,又測得C對于山坡的斜度為45°,若CD=50m,山坡對于地平面的坡度為θ,則cosθ=$\sqrt{3}$-1.
如圖所示,在坡度一定的山坡A處測得山頂上一建筑物CD的頂端C對于山坡的斜度為15°,向山頂前進100m到達B處,又測得C對于山坡的斜度為45°,若CD=50m,山坡對于地平面的坡度為θ,則cosθ=$\sqrt{3}$-1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com