
【題目】已知函數f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的單調性,并證明你的結論;
(3)若f(x)為奇函數,求滿足f(ax)<f(2)的x的取值范圍.
【答案】(1)f(0)=a-1;(2)見解析;(3)(-∞,2).
【解析】試題分析:(1)代入x=0即可得值;
(2)利用單調性的定義任取x1,x2∈R,且x1<x2,判斷f(x1)-f(x2)與0的大小即可;
(3)由奇函數的定義f(-x)=-f(x),得a=1,進而由函數單調性解不等式即可.
試題解析:
(1)f(0)=a-![]() =a-1.
=a-1.
(2)∵f(x)的定義域為R,
∴任取x1,x2∈R,且x1<x2,
則f(x1)-f(x2)=a-![]() -a+
-a+![]()
=![]() .
.
∵y=2x在R上單調遞增,且x1<x2,
∴0<2x1<2x2,
∴2x1-2x2<0,2x1+1>0,2x2+1>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),∴f(x)在R上單調遞增.
(3)∵f(x)是奇函數,
∴f(-x)=-f(x),
即a-![]() =-a+
=-a+![]() ,解得a=1.
,解得a=1.
[或用f(0)=0求解]
∴f(ax)<f(2)即為f(x)<f(2).
又∵f(x)在R上單調遞增,
∴x<2.(或代入化簡亦可)
故x的取值范圍為(-∞,2).


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】為了預防流感,某學校對教室用藥熏消毒法進行消毒,已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系式為![]() (a為常數),如圖所示.根據圖中提供的信息,回答下列問題:
(a為常數),如圖所示.根據圖中提供的信息,回答下列問題:

(1)從藥物釋放開始,每立方米空氣中的含藥量y(毫克)與時間t(小時)之間的函數關系式為_________;
(2)據測定,當空氣中每立方米的含藥量降低到0.25毫克以下時,學生方可進教室,那么從藥物釋放開始,至少需要經過_________小時后,學生才能回到教室.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第![]() 屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
第 | 第 | 第 | 第 | 第 | |
中國 |
|
|
|
|
|
俄羅斯 |
|
|
|
|
|
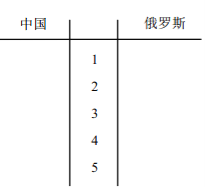
(1)根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖, 并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度( 不要求計算出具體數值, 給出結論即可);
(2)甲、 乙、 丙三人競猜今年中國代表團和俄羅斯代表團中的哪一個獲得的金牌數多( 假設兩國代表團獲得的金牌數不會相等) , 規定甲、 乙、 丙必須在兩個代表團中選一個, 已知甲、 乙猜中國代表團的概率都為![]() , 丙猜中國代表團的概率為
, 丙猜中國代表團的概率為![]() , 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為
, 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大家知道, 莫言是中國首位獲得諾貝爾獎的文學家, 國人歡欣鼓舞.某高校文學社從男女生中各抽取![]() 名同學調查對莫言作品的了解程度, 結果如下:
名同學調查對莫言作品的了解程度, 結果如下:
閱讀過莫言的作品數( 篇) |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(1)試估計該校學生閱讀莫言作品超過![]() 篇的概率;
篇的概率;
(2)對莫言作品閱讀超過![]() 篇的則稱為“對莫言作品非常了解” , 否則為“ 一般了解” .根據題意完成下表, 并判斷能否在犯錯誤的概率不超過
篇的則稱為“對莫言作品非常了解” , 否則為“ 一般了解” .根據題意完成下表, 并判斷能否在犯錯誤的概率不超過![]() 的前提下, 認為對莫言作品非常了解與性別有關?
的前提下, 認為對莫言作品非常了解與性別有關?
非常了解 | 一般了解 | 合計 | |
男生 | |||
女生 | |||
合計 |
附: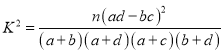 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為加快新能源汽車產業發展,推進節能減排,國家鼓勵消費者購買新能源汽車,某校研究性學習小組,從汽車市場上隨機選取了![]() 輛純電動乘用車,根據其續駛里程
輛純電動乘用車,根據其續駛里程![]() (單次充電后能行駛的最大里程)作出了頻率與頻數的統計表:
(單次充電后能行駛的最大里程)作出了頻率與頻數的統計表:
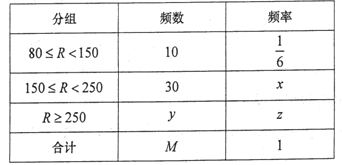
(1)求![]() 的值;
的值;
(2)若用分層抽樣的方法從這![]() 輛純電動乘用車中抽取一個容量為6的樣本,從該樣本中任選2輛,求選到的2輛車續駛里程為
輛純電動乘用車中抽取一個容量為6的樣本,從該樣本中任選2輛,求選到的2輛車續駛里程為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究家用轎車在高速公路上的車速情況,交通部門隨機對50名家用轎車駕駛員進行調查,得到其在高速公路上行駛時的平均車速情況為:在30名男性駕駛員中,平均車速超過![]() 的有20人,不超過
的有20人,不超過![]() 的有10人.在20名女性駕駛員中,平均車速超過
的有10人.在20名女性駕駛員中,平均車速超過![]() 的有5人,不超過
的有5人,不超過![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列聯表,并判斷是否有99.5%的把握認為平均車速超過![]() 的人與性別有關;
的人與性別有關;
平均車速超過
| 平均車速不超過
| 合計 | |
男性駕駛員人數 | |||
女性駕駛員人數 | |||
合計 |
(Ⅱ )以上述數據樣本來估計總體,現從高速公路上行駛的大量家用轎車中隨機抽取3輛,記這3輛車中駕駛員為女性且車速不超過![]() 的車輛數為
的車輛數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: ![]() ,其中
,其中![]() .
.
參考數據:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com