
(本小題滿分13分)已知數列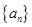 的前
的前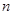 項和是
項和是 ,且
,且 .
.
(Ⅰ)求數列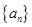 的通項公式;
的通項公式;
(Ⅱ)記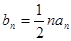 ,求數列
,求數列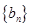 的前
的前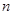 項和
項和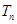 .
.
(Ⅰ) ; (Ⅱ)
; (Ⅱ) 。
。
解析試題分析:(I)先令n=1,得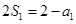 ,從而得到
,從而得到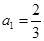 .
.
然后再令 時,由
時,由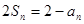 得:
得: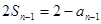 ,兩式相減得:
,兩式相減得:
即 ,從而確定
,從而確定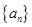 為等比數列,問題得解.
為等比數列,問題得解.
(II)在(I)的基礎上,可求出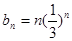 ,顯然應采用錯位相減的方法求和即可.
,顯然應采用錯位相減的方法求和即可.
(Ⅰ)當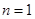 時,
時, 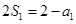 ,
,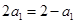 ,∴
,∴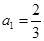 ; ………… 2分
; ………… 2分
當 時,由
時,由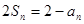 得:
得: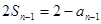
兩式相減得:
即 ,又
,又
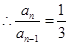
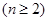 , ……………… 5分
, ……………… 5分
∴數列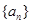 是以
是以 為首項,
為首項,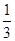 為公比的等比數列. ………………… 6分
為公比的等比數列. ………………… 6分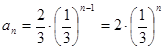 ………………… 7分
………………… 7分
(Ⅱ)由(Ⅰ)知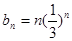 , ………………… 8分
, ………………… 8分
∴ …………………①
…………………①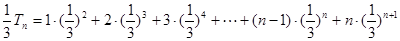 …………②
…………②
由①-②得: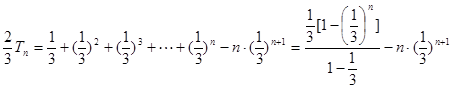
…………………9分 ………………… 12分
………………… 12分 ………………… 13分
………………… 13分
考點: 由an與Sn的關系求出an,等比數列的定義,通項公式,錯位相減法求和.
點評:(I)再由Sn求an時,應先確定a1,然后再根據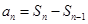 ,求
,求 時,an.
時,an.
(II)當一個數列的通項是一個等差數列與一個等比數列積時,可以采用錯位相減法求和.


 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知曲線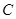 :
: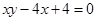 ,數列
,數列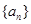 的首項
的首項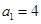 ,且當
,且當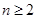 時,點
時,點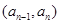 恒在曲線
恒在曲線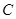 上,數列
上,數列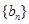 滿足
滿足 。
。
(1)試判斷數列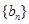 是否是等差數列?并說明理由;
是否是等差數列?并說明理由;
(2)求數列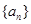 和
和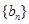 的通項公式;
的通項公式;
(3)設數列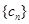 滿足
滿足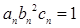 ,試比較數列
,試比較數列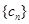 的前
的前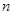 項和
項和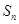 與2的大小。
與2的大小。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)(注意:在試題卷上作答無效)
已知曲線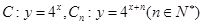 ,從
,從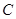 上的點
上的點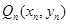 作
作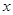 軸的垂線,交
軸的垂線,交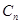 于點
于點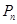 ,再從點
,再從點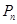 作
作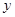 軸的垂線,交
軸的垂線,交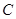 于點
于點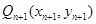 ,設
,設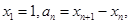
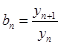
(1)求數列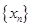 的通項公式;
的通項公式;
(2)記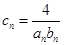 ,數列
,數列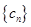 的前
的前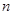 項和為
項和為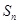 ,試比較
,試比較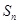 與
與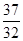 的大小
的大小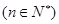 ;
;
(3)記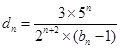 ,數列
,數列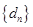 的前
的前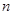 項和為
項和為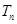 ,試證明:
,試證明: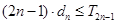
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某少數民族的刺繡有著悠久的歷史,如下圖(1)、(2)、(3)、(4)為她們刺繡最簡單的四個圖案,這些圖案都是由小正方形構成,小正方形數越多刺繡越漂亮.現按同樣的規律刺繡(小正方形的擺放規律相同),設第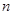 個圖形包含
個圖形包含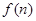 個小正方形.
個小正方形.
(1)求出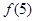 的值;
的值;
(2)利用合情推理的“歸納推理思想”,歸納出 與
與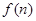 之間的關系式,并根據你得到的關系式求出
之間的關系式,并根據你得到的關系式求出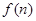 的表達式;
的表達式;
(3)求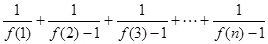 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com