
橢圓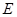 :
: 的右焦點
的右焦點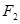 與拋物線
與拋物線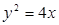 的焦點重合,過
的焦點重合,過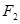 作與
作與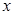 軸垂直的直線
軸垂直的直線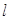 與橢圓交于
與橢圓交于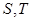 兩點,與拋物線交于
兩點,與拋物線交于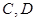 兩點,且
兩點,且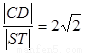 。
。
(1)求橢圓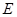 的方程;
的方程;
(2)若過點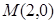 的直線與橢圓
的直線與橢圓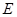 相交于兩點
相交于兩點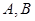 ,設(shè)
,設(shè) 為橢圓
為橢圓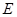 上一點,且滿足
上一點,且滿足
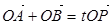
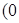 為坐標(biāo)原點),當(dāng)
為坐標(biāo)原點),當(dāng)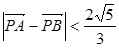 時,求實數(shù)
時,求實數(shù)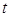 的取值范圍。
的取值范圍。
(1) 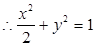 (2)
(2) 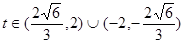
【解析】
試題分析:(1)設(shè)橢圓的半長軸、半短軸、半焦距為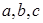 ,則
,則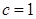 ,且
,且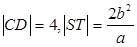 ,
,
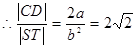 ,又
,又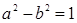 ,
,
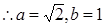 ,
,
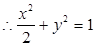 ——————————————————————————————6分
——————————————————————————————6分
(2)由題,直線 斜率存在,設(shè)直線
斜率存在,設(shè)直線 :
: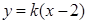 ,聯(lián)立
,聯(lián)立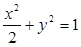 ,消
,消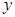 得:
得:
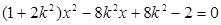 ,由
,由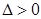 ,得
,得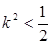 ①————————8分
①————————8分
設(shè)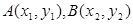 ,由韋達(dá)定理得
,由韋達(dá)定理得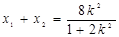 ,
,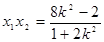
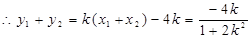 ,
,
則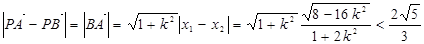
 或
或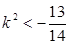 (舍)②
(舍)②
由 ①②得:
①②得: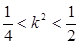 ——————————————————————————11分
——————————————————————————11分
則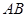 的中點
的中點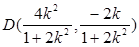
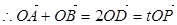 ,得
,得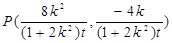 代入橢圓方程得:
代入橢圓方程得:
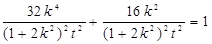 ,即
,即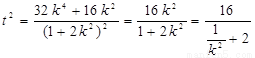
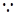
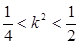 ,
,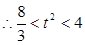 ,即
,即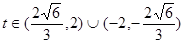 ————————15分
————————15分
考點:橢圓方程,直線與橢圓位置關(guān)系
點評:根據(jù)圓錐曲線的性質(zhì)求解橢圓的方程,同時能聯(lián)立方程組來得到交點坐標(biāo)的關(guān)系,結(jié)合韋達(dá)定理來分析求解,屬于中檔題。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年福建省三明市畢業(yè)班5月質(zhì)量檢查理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知橢圓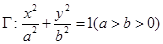 的離心率為
的離心率為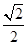 ,且橢圓
,且橢圓 的右焦點
的右焦點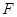 與拋物線
與拋物線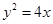 的焦點重合.
的焦點重合.
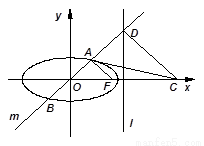
(Ⅰ)求橢圓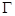 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)如圖,設(shè)直線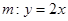 與橢圓
與橢圓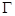 交于
交于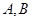 兩點(其中點
兩點(其中點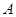 在第一象限),且直線
在第一象限),且直線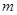 與定直線
與定直線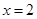 交于點
交于點 ,過
,過 作直線
作直線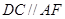 交
交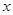 軸于點
軸于點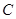 ,試判斷直線
,試判斷直線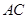 與橢圓
與橢圓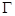 的公共點個數(shù).
的公共點個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆廣東省東莞市高二3月月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知橢圓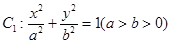 的右焦點
的右焦點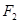 與拋物線
與拋物線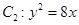 的焦點重合,左端點為
的焦點重合,左端點為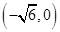
(1)求橢圓的方程;
(2)過橢圓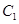 的右焦點且斜率為
的右焦點且斜率為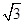 的直線
的直線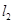 被橢圓
被橢圓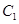 截的弦長
截的弦長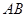 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:廣東省09-10學(xué)年高二下學(xué)期期末考試?yán)砜茢?shù)學(xué)試題 題型:選擇題
設(shè)橢圓 的右焦點與拋物線
的右焦點與拋物線 的焦點相同,離心率為
的焦點相同,離心率為 ,則此橢圓的方程為
,則此橢圓的方程為
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年福建省福州市高三第五次質(zhì)量檢查數(shù)學(xué)理卷 題型:選擇題
設(shè)橢圓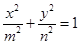 (
(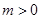 ,
,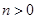 )的右焦點與拋物線
)的右焦點與拋物線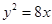 的焦點相同,離心率為
的焦點相同,離心率為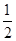 ,則此橢圓的方程為
,則此橢圓的方程為
A.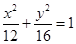 B.
B.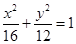 C.
C. D.
D.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com