
記數列{ }的前n項和為為
}的前n項和為為 ,且
,且 +
+ +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求證:數列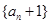 是等比數列;
是等比數列;
(2)已知2是函數f(x)=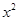 +ax-1的零點,若關于x的不等式f(x)≥
+ax-1的零點,若關于x的不等式f(x)≥ 對任意n∈N﹡在x∈(-∞,λ]上恒成立,求實常數λ的取值范圍.
對任意n∈N﹡在x∈(-∞,λ]上恒成立,求實常數λ的取值范圍.
 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)是定義在R上的奇函數,且f(x)的圖象關于直線x=1對稱.
(1)求證:f(x)是周期為4的周期函數;
(2)若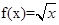 (0<x≤1),求x∈[-5,-4]時,函數f(x)的解析式.
(0<x≤1),求x∈[-5,-4]時,函數f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知定義在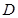 上的函數
上的函數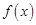 ,如果滿足:對任意
,如果滿足:對任意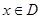 ,存在常數
,存在常數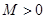 ,使得
,使得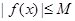 成立,則稱
成立,則稱 是
是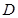 上的有界函數,其中
上的有界函數,其中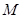 稱為函數
稱為函數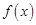 的上界.
的上界.
下面我們來考慮兩個函數: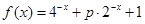 ,
,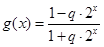 .
.
(Ⅰ)當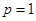 時,求函數
時,求函數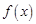 在
在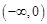 上的值域,并判斷函數
上的值域,并判斷函數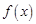 在
在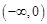 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(Ⅱ)若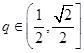 ,函數
,函數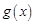 在
在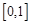 上的上界是
上的上界是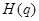 ,求
,求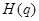 的取值范圍;
的取值范圍;
(Ⅲ)若函數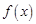 在
在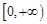 上是以
上是以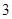 為上界的有界函數, 求實數
為上界的有界函數, 求實數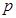 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
停車場預計“十·一”國慶節這天將停放大小汽車1200輛次,該停車場的收費標準為:大車每輛次10元,小車每輛次5元.根據預計,解答下面的問題:
(1)寫出國慶節這天停車場的收費金額y(元)與小車停放輛次x(輛)之間的函數關系式,并指出自變量x的取值范圍;
(2)如果國慶節這天停放的小車輛次占停車總輛次的65%~85%,請你估計國慶節這天該停車場收費金額的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在股票市場上,投資者常參考股價(每一股的價格)的某條平滑均線的變化情況來決定買入或賣出股票。股民老張在研究股票的走勢圖時,發現一只股票的均線近期走得很有特點:如果按如圖所示的方式建立平面直角坐標系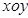 ,則股價
,則股價 (元)和時間
(元)和時間 的關系在
的關系在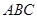 段可近似地用解析式
段可近似地用解析式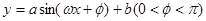 來描述,從
來描述,從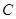 點走到今天的
點走到今天的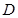 點,是震蕩筑底階段,而今天出現了明顯的筑底結束的標志,且
點,是震蕩筑底階段,而今天出現了明顯的筑底結束的標志,且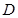 點和
點和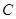 點正好關于直線
點正好關于直線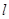 :
: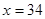 對稱。老張預計這只股票未來的走勢如圖中虛線所示,這里
對稱。老張預計這只股票未來的走勢如圖中虛線所示,這里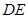 段與
段與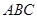 段關于直線
段關于直線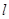 對稱,
對稱,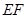 段是股價延續
段是股價延續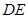 段的趨勢(規律)走到這波上升行
段的趨勢(規律)走到這波上升行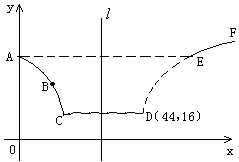
情的最高點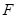 。現在老張決定取點
。現在老張決定取點
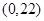 ,點
,點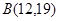 ,點
,點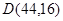 來確定解析式中的常數
來確定解析式中的常數 ,
,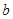 ,
,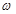 ,
,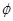 ,并且求得
,并且求得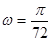 。
。
(Ⅰ)請你幫老張算出 ,
,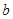 ,
,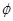 ,并回答股價什么時候見頂(即求
,并回答股價什么時候見頂(即求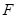 點的橫坐標)
點的橫坐標)
(Ⅱ)老張如能在今天以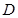 點處的價格買入該股票3000股,到見頂處
點處的價格買入該股票3000股,到見頂處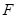 點的價格全部賣出,不計其它費用,這次操作他能賺多少元?
點的價格全部賣出,不計其它費用,這次操作他能賺多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某投資公司投資甲、乙兩個項目所獲得的利潤分別是P(億元)和Q億元),它們與投資額t(億元)的關系有經驗公式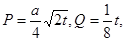 其中
其中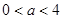 ,今該公司將5億元投資這兩個項目,其中對甲項目投資x(億元),投資這兩個項目所獲得的總利潤為y(億元),
,今該公司將5億元投資這兩個項目,其中對甲項目投資x(億元),投資這兩個項目所獲得的總利潤為y(億元),
(1)求y關于x的解析式,
(2)怎樣投資才能使總利潤最大,最大值為多少?.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com