
設F1、F2為橢圓![]() 的兩個焦點,P為上一點,已知P、F1、F2是一個直角三角形的三個頂點,且|PF1|>|PF2|,求
的兩個焦點,P為上一點,已知P、F1、F2是一個直角三角形的三個頂點,且|PF1|>|PF2|,求![]() 的值.
的值.
由已知,|PF1|>|PF2|,|PF1|+|PF2|=6,|F1F2|=![]() ,
,
若∠PF2F1為直角,則|PF1|2=|PF2|2+|F1F2|2,可解得:|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,這時
,這時![]() .
.
若∠F2PF1為直角,則|PF1|2+|PF2|2=|F1F2|2,可解得:|PF1|=4,|PF2|=2,這時![]() .
.
解法2:由橢圓的對稱性,不妨設P(x,y)(其中x>0,y>0),![]() .若∠PF2F1為直角,則P(
.若∠PF2F1為直角,則P(![]() ),這時|PF1|=
),這時|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,這時
,這時![]() .若∠PF2F1為直角,則由
.若∠PF2F1為直角,則由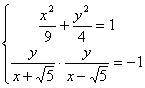 ,解得:
,解得:![]() .
.
于是|PF1|=4,|PF2|=2,這時![]() .
.
點評:由橢圓的方程,熟練準確地寫出其幾何性質(如頂點,焦點,長、短軸長,焦距,離心率,焦半徑等)是應對考試必備的基本功;在解法2中設出了P點坐標的前提下,還可利用|PF1|=a+ex,|PF2|=a-ex來求解.
由已知,F1不是直角頂點,所以只要對P、F2中哪一個是直角頂點分兩種情況即可.


科目:高中數學 來源: 題型:
| x2 |
| 4 |
| PF1 |
| PF2 |
| A、0 | B、2 | C、4 | D、-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| 9 |
| y2 |
| 4 |
| |PF1| |
| |PF2| |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| 4 |
| y2 |
| 3 |
| PF1 |
| PF2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com