
分析 (1)由外確界與內確界的概念,結合曲線方程,即可求出答案.
(2)由外確界與內確界的概念,結合曲線方程,即可求出答案.
(2)由題意求出曲線C的方程,進一步得到x的范圍,把x2+y2轉化為含有x的代數式,分類討論得答案.
解答 解.(1)曲線x+y=1(0<x<4)的外確界M0=5與內確界${m_0}=\frac{{\sqrt{2}}}{2}$.
(2)對于曲線y2=4x,設P(x,y)為曲線上任意一點$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{{x^2}+4x}=\sqrt{{{(x+2)}^2}-4}(x≥0)$,
∴|OP|∈[0,+∞),
∴曲線y2=4x不是有界曲線.
對于曲線(x-1)2+y2=4$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{{x^2}+4-{{(x-1)}^2}}=\sqrt{2x+3}(-1≤x≤3)$,
∴|OP|∈[1,3],
∴曲線(x-1)2+y2=4是有界曲線,外確界M0=3與內確界m0=1.
(3)由已知得:$\sqrt{{{(x-1)}^2}+{y^2}}×\sqrt{{{(x+1)}^2}+{y^2}}=a$$\sqrt{{x^2}-2x+1+{y^2}}×\sqrt{{x^2}+2x+1+{y^2}}=\sqrt{{{({x^2}+{y^2}+1)}^2}-4{x^2}}=a$,
∴(x2+y2+1)2-4x2=a2,
∴${y^2}=\sqrt{4{x^2}+{a^2}}-({x^2}+1)$,
∵y2≥0,
∴$\sqrt{4{x^2}+{a^2}}≥{x^2}+1$,
∴(x2+1)2≤4x2+a2,
∴(x2-1)2≤a2,
∴1-a≤x2≤a+1,
∵$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{\sqrt{4{x^2}+{a^2}}-1}$
若0<a<1,則$\sqrt{1-a}≤\sqrt{\sqrt{4{x^2}+{a^2}}-1}≤\sqrt{a+1}$,外確界${M_0}=\sqrt{a+1}$,內確界${m_0}=\sqrt{1-a}$
若a≥1,0≤x2≤a+1,則$\sqrt{a-1}≤\sqrt{\sqrt{4{x^2}+{a^2}}-1}≤\sqrt{a+1}$,外確界${M_0}=\sqrt{a+1}$,內確界${m_0}=\sqrt{a-1}$
綜合得:外確界${M_0}=\sqrt{a+1}$,內確界${m_0}=\sqrt{|a-1|}$.
點評 本題考查曲線的外確界與內確界的求法,體現了分類討論的數學思想方法,理解題意是關鍵,注意函數與方程思想的合理運用,屬難題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
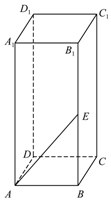 如圖所示,長方體ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是側棱BB1的中點.過點A1,D1,E的平面α與此長方體的面相交,交線圍成一個四邊形.
如圖所示,長方體ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是側棱BB1的中點.過點A1,D1,E的平面α與此長方體的面相交,交線圍成一個四邊形.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com