日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
若△ABC中，sinA：sinB：sinC=2：3：4，那么cosC=（ ）
A．
B．
C．
D．
【答案】分析：通過正弦定理求出，a：b：c=2：3：4，設出a，b，c，利用余弦定理直接求出cosC即可．
解答：解：因為sinA：sinB：sinC=2：3：4
所以a：b：c=2：3：4，設a=2k，b=3k，c=4k
由余弦定理可知：
cosC===-．
故選A．
點評：本題是基礎題，考查正弦定理與余弦定理的應用，考查計算能力．
練習冊系列答案
相關習題

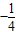
科目：高中數學 來源： 題型：

△ABC中，sin(
π
2
+B)=
2
5
5
，a，b，c分別是角A，B，C的對邊．
（1）求tanB；
（2）若sinA=
10
10
，c=10，△ABC的面積．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知
a
=（1+cosα，sinα），
b
=（1-cosβ，sinβ），
c
=(1，0)，α∈（0，π），β∈（π，2π），向量
a
與
c
夾角為θ1，向量
b
與
c
夾角為θ2，且θ1-θ2=
π
6
，若△ABC中角A、B、C的對邊分別為a、b、c，且角A=β-α．
求（Ⅰ）求角A 的大小； 
（Ⅱ）若△ABC的外接圓半徑為4
3
，試求b+c取值范圍．

查看答案和解析>>

科目：高中數學 來源：2012年江蘇省南京外國語學校高考數學沖刺模擬試卷（解析版） 題型：解答題

已知=（1+cosα，sinα），=（1-cosβ，sinβ），，α∈（0，π），β∈（π，2π），向量與夾角為θ1，向量與夾角為θ2，且θ1-θ2=，若△ABC中角A、B、C的對邊分別為a、b、c，且角A=β-α．
求（Ⅰ）求角A 的大小； 
（Ⅱ）若△ABC的外接圓半徑為，試求b+c取值范圍．

查看答案和解析>>

科目：高中數學 來源：2012年江蘇省高考數學全真模擬試卷（8）（解析版） 題型：解答題

已知=（1+cosα，sinα），=（1-cosβ，sinβ），，α∈（0，π），β∈（π，2π），向量與夾角為θ1，向量與夾角為θ2，且θ1-θ2=，若△ABC中角A、B、C的對邊分別為a、b、c，且角A=β-α．
求（Ⅰ）求角A 的大小； 
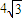（Ⅱ）若△ABC的外接圓半徑為，試求b+c取值范圍．

查看答案和解析>>

科目：高中數學 來源：2011年江蘇省南通市如東高級中學高考數學模擬試卷（1）（解析版） 題型：解答題

已知=（1+cosα，sinα），=（1-cosβ，sinβ），，α∈（0，π），β∈（π，2π），向量與夾角為θ1，向量與夾角為θ2，且θ1-θ2=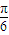，若△ABC中角A、B、C的對邊分別為a、b、c，且角A=β-α．
求（Ⅰ）求角A 的大小； 
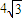（Ⅱ）若△ABC的外接圓半徑為，試求b+c取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 91视频8mav | 国产剧情一区二区 | 国产精品一区久久久久 | 中文字幕久久久 | 欧美激情视频久久 | 日本视频在线免费观看 | 中文字幕av一区二区三区 | 综合久久综合久久 | 久草 在线 | 日韩欧美一二三区 | 中文字幕在线一区二区三区 | av一区二区在线播放 | 欧美精品在线一区二区三区 | 日本免费福利视频 | 影音先锋亚洲资源 | 97成人精品视频在线观看 | 色婷婷综合久久久久中文 | 精品国产aⅴ一区二区 | 一区二区视频 | 欧美一级精品片在线看 | 一区网站| 欧美一区永久视频免费观看 | 国产一区二区在线播放 | 一区不卡在线观看 | 欧美性一区二区三区 | 精品国产成人 | 国产精品久久久久久久久免费高清 | 免费激情小视频 | 91麻豆精品一区二区三区 | 亚洲精品视频在线看 | 久久久久国产一区二区三区 | 欧美精品1区2区 | 国产午夜久久久久 | 亚洲欧美国产一区二区 | 久久久久久久久久久一区二区 | 欧美一区二区三区啪啪 | 国产精品一区久久久久 | 亚洲精品久久久久久久久久久 | 一区二区三区在线播放 | а天堂中文最新一区二区三区 | 中文av电影 |