
(本題滿分12分)
過拋物線![]() 上不同兩點(diǎn)A、B分別作拋物線的切線相交于P點(diǎn),
上不同兩點(diǎn)A、B分別作拋物線的切線相交于P點(diǎn),![]()
(Ⅰ)求證:P點(diǎn)的軌跡為一條直線;
(Ⅱ)已知點(diǎn)F(0,1),是否存在實(shí)數(shù)![]() 使得
使得![]() ?
?
若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(本小題滿分12分)
證法(一):(Ⅰ)設(shè)![]()
由![]() 得:
得:![]()
![]()
![]() ………………………………3分
………………………………3分
直線PA的方程是:![]() 即
即![]() ①
①
同理,直線PB的方程是:![]() ②
②
由①②得: ∴點(diǎn)P的軌跡方程是
∴點(diǎn)P的軌跡方程是![]() ……6分
……6分
(Ⅱ)由(1)得:![]()
![]()
![]()
![]()
![]() …………………………10分
…………………………10分
![]()
所以![]()
故存在![]() =1使得
=1使得![]() …………………………………………12分
…………………………………………12分
證法(二):(Ⅰ)∵直線PA、PB與拋物線相切,且![]()
∴直線PA、PB的斜率均存在且不為0,且![]()
設(shè)PA的直線方程是![]()
由![]() 得:
得:![]()
![]() 即
即![]() …………………………3分
…………………………3分
即直線PA的方程是:![]()
同理可得直線PB的方程是:![]()
由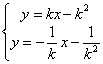 得:
得: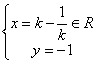
故點(diǎn)P的軌跡方程是![]() ……………………………………6分
……………………………………6分
(Ⅱ)由(1)得:![]()
![]()
![]()
![]() ………………………………10分
………………………………10分
![]()
故存在![]() =1使得
=1使得![]() …………………………………………12分
…………………………………………12分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| π | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本題滿分12分)已知數(shù)列![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公比
,公比![]() 的等比數(shù)列,,
的等比數(shù)列,,
設(shè)![]() ,數(shù)列
,數(shù)列![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;(2)求數(shù)列
的通項(xiàng)公式;(2)求數(shù)列![]() 的前n項(xiàng)和Sn.
的前n項(xiàng)和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年上海市金山區(qū)高三上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分12分,第1小題6分,第2小題6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求實(shí)數(shù)a的取值范圍.
,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年安徽省高三10月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分12分)
設(shè)函數(shù) (
( ,
, 為常數(shù)),且方程
為常數(shù)),且方程 有兩個(gè)實(shí)根為
有兩個(gè)實(shí)根為 .
.
(1)求 的解析式;
的解析式;
(2)證明:曲線 的圖像是一個(gè)中心對稱圖形,并求其對稱中心.
的圖像是一個(gè)中心對稱圖形,并求其對稱中心.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年重慶市高三第二次月考文科數(shù)學(xué) 題型:解答題
(本題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問6分,(Ⅲ)小問2分.)
如圖所示,直二面角 中,四邊形
中,四邊形 是邊長為
是邊長為 的正方形,
的正方形, ,
, 為
為 上的點(diǎn),且
上的點(diǎn),且 ⊥平面
⊥平面
(Ⅰ)求證: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求點(diǎn) 到平面
到平面 的距離.
的距離.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com