【題目】已知函數
（1）討論
的極值；
（2）若
對任意
恒成立，求實數
的取值范圍.
【答案】（Ⅰ）當
時，
無極值；當
時，有極大值
，無極小值；（Ⅱ）
【解析】
【試題分析】（1）先對函數
，
求導，再分和兩種情形討論導函數值
（
）的符號，進而判定函數單調區間，求出函數的極值；（2）先將原不等式
等價轉化為
，進而構造函數
（
），將問題轉化為求出
.然后借助題設條件先對函數（）求導，再對實數
分類運用導數的知識求出
=0，進而確定所求實數的取值范圍。
解：（Ⅰ）依題意（），
①當時，
，在
上單調遞增，無極值；
②當時，
，
當
時，，在
上單調遞增；
當
時，，在
上單調遞增；
所以
，無極小值.
綜上可知，當時，無極值；當時，有極大值
，無極小值.
（Ⅱ）原不等式可化為
，
記（），只需
.
可得
.
（1）當時，
，
，所以
，
在
上單調遞增，所以當
時，
，不合題意，舍去.
（2）當時，
，
①當時，因為，所以
，所以
，
所以在上單調遞減.
故當時，
，符合題意.
②當
時，記
（），
所以
，
在上單調遞減.
又
，
，
所以存在唯一
，使得
.
當
時，
，
從而
，即在
上單調遞增，
所以當時，，不符合要求，舍去.
綜上可得，.
舉一反三期末百分沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數
的圖象與x軸交點為
，與此交點距離最小的最高點坐標為
.
（Ⅰ）求函數
的表達式；
（Ⅱ）若函數滿足方程
，求方程在
內的所有實數根之和；
（Ⅲ）把函數
的圖像的周期擴大為原來的兩倍，然后向右平移
個單位，再把縱坐標伸長為原來的兩倍，最后向上平移一個單位得到函數
的圖像．若對任意的
，方程
在區間
上至多有一個解，求正數k的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列敘述中正確的是( )
A. 若
，則“
”的充要條件是“
”
B. 函數
的最大值是
C. 命題“
”的否定是“
”
D. 
是一條直線，
是兩個不同的平面，若
則
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，直角梯形公園
中，
，
，
，公園的左下角陰影部分為以
為圓心，半徑為
的
圓面的人工湖，現設計修建一條與圓相切的觀光道路
（點
分別在
與
上），
為切點，設
.
（1）試求觀光道路長度的最大值；
（2）公園計劃在道路的右側種植草坪，試求草坪
的面積最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為調查某地區老年人是否需要志愿者提供幫助，用簡單隨機抽樣的方法從該地區調查了500位老年人，結果如下：
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附：
的觀測值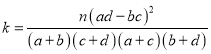
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（1）估計該地區老年人中，需要志愿者提供幫助的老年人的比例；
（2）在犯錯誤的概率不超過0.01的前提下是否可認為該地區的老年人是否需要志愿者提供幫助與性別有關？
查看答案和解析>>
科目：高中數學 來源： 題型：
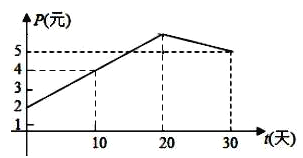
【題目】某上市股票在30天內每股的交易價格P（元）與時間t（天）組成有序數對
，點落在如圖所示的兩條線段上.該股票在30天內（包括30天）的日交易量M（萬股）與時間t（天）的部分數據如下表所示：
第t天 | 6 | 13 | 20 | 27 |
M（萬股） | 34 | 27 | 20 | 13 |
（1）根據提供的圖象，寫出該股票每股交易價格P（元）與時間t（天）所滿足的函數關系式
______；
（2）根據表中數據，寫出日交易量M（萬股）與時間t（天）的一次函數關系式：
______；
（3）用y（萬元）表示該股票日交易額，寫出y關于t的函數關系式，并求在這30天內第幾天日交易額最大，最大值為多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
