已知函書f(x)=2x2+k|x-1|(k∈R)
(1)若k=-1,求方程f(x)=4的實數解;
(2)若k=6,求函數f(x)的單調區間
(3)若f(x)的最小值是f(1)=2,求k的范圍.
解:(1)若k=-1,則方程f(x)=4即為:2x
2-|x-1|=4
當x≥1時,方程可化為(x+1)(2x-3)=0,∴

;
當x<1時,方程可化為2x
2+x-5=0,∴
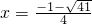
(2)若k=6,則函數f(x)=2x
2+6|x-1|=
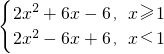
∵
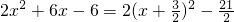
,∴函數在[1,+∞)上為單調增函數;
∵
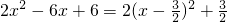
,∴函數在(-∞,1)上為單調減函數;
∴k=6時,函數的單調減區間為(-∞,1),函數的單調增區間為[1,+∞)
(3)由(2)分析知,函數在(-∞,1)上為單調減函數;函數在[1,+∞)上為單調增函數
∵f(x)=2x
2+k|x-1|=
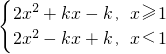
∴
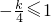
且
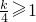
∴k≥4
分析:(1)若k=-1,則方程f(x)=4即為:2x
2-|x-1|=4,再將絕對值符號化去,分類討論,解方程即可;
(2)若k=6,將函數化簡,f(x)=2x
2+6|x-1|=
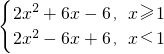
,分別利用配方法,即可得到函數的單調減區間為(-∞,1),函數的單調增區間為[1,+∞);
(3)由(2)分析知,函數在(-∞,1)上為單調減函數;函數在[1,+∞)上為單調增函數,將函數化簡f(x)=2x
2+k|x-1|=
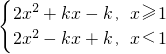
,根據函數的單調性可得
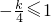
且
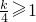
,從而可求k的范圍.
點評:本題以二次函數為載體,考查方程的解,函數的單調區間,考查解不等式,解題的關鍵是利用零點將絕對值符號化去,從而利用二次函數的性質解題.

 ;
;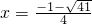
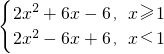
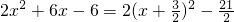 ,∴函數在[1,+∞)上為單調增函數;
,∴函數在[1,+∞)上為單調增函數;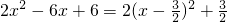 ,∴函數在(-∞,1)上為單調減函數;
,∴函數在(-∞,1)上為單調減函數;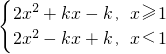
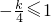 且
且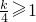
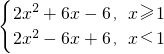 ,分別利用配方法,即可得到函數的單調減區間為(-∞,1),函數的單調增區間為[1,+∞);
,分別利用配方法,即可得到函數的單調減區間為(-∞,1),函數的單調增區間為[1,+∞);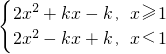 ,根據函數的單調性可得
,根據函數的單調性可得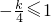 且
且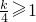 ,從而可求k的范圍.
,從而可求k的范圍.
