
分析 (Ⅰ)求出函數的導數,解關于導函數的不等式,求出函數的單調區間,從而求出函數的零點個數即可;
(Ⅱ)要證x1+x2<2,只需證x1<2-x2,只需證f(x1)>f(2-x2),即要證f(2-x2)<0,令h(x)=-xe2-x-(x-2)ex,根據函數的單調性證明即可;
解答 解:(I)由g(x)=0得a=(2-x)ex,令g(x)=(2-x)ex,
函數f(x)的零點個數即直線y=a與曲線g(x)=(2-x)ex的交點個數,
∵g'(x)=-ex+(2-x)ex=(1-x)ex,-------------(2分)
由g'(x)>0得x<1,∴函數g(x)在(-∞,1)單調遞增,
由g'(x)<0得x>1,∴函數g(x)在(1,+∞)上單調遞減,
∴當x=1時,函數g(x)有最大值,g(x)max=g(1)=e,----------------------------------------(3分)
又當x<2時,g(x)>0,g(2)=0,當x>2時g(x)<0,
∴當a>e時,函數f(x)沒有零點;----------------------------------------------------------------(4分)
當a=e或a≤0時,函數f(x)有一個零點;------------------------------------------------------(5分)
當0<a<e時,函數f(x)有兩個零點.------------------------------------------------------------(6分)
(II)證明:函數f(x)的零點即直線y=a與曲線g(x)=(2-x)ex的交點橫坐標,
不妨設x1<x2,由(I)知x1<1,x2>1,得2-x2<1,
∵函數g(x)=(2-x)ex在(-∞,1)上單調遞增,
∴函數f(x)=-g(x)+a在(-∞,1)單調遞減,
要證x1+x2<2,只需證x1<2-x2,------------------------------------------------------------(7分)
∴只需證f(x1)>f(2-x2),又f(x1)=0,即要證f(2-x2)<0,---------------------(8分)
∵由a=g(x2)得$f(2-{x_2})=-{x_2}{e^{2-{x_2}}}+a=-{x_2}{e^{2-{x_2}}}-({x_2}-2){e^{x_2}}$,(x2>1)--------(9分)
令h(x)=-xe2-x-(x-2)ex,則h'(x)=(1-x)(ex-e2-x),------------------------------(10分)
當x>1時,ex>e2-x,h'(x)<0,即函數h(x)在(1,+∞)上單調遞減,
∴h(x)<h(1)=0,
∴當x2>1時,f(2-x2)<0,即x1+x2<2.------------------------------------------------(12分)
證法二:由(Ⅰ)知,a>0,不妨設x1<1<x2,
設F(x)=f(x)-f(2-x)(x>1),則F(x)=(x-2)ex+xe2-x,-----------------------------(8分)
F'(x)=(1-x)(e2-x-ex),易知y=e2-x-ex是減函數,
當x>1時,e2-x-ex<e-e=0,又1-x<0,得F'(x)>0,
所以F(x)在(1,+∞)遞增,F(x)>F(1)=0,即f(x)>f(2-x).---------------------------(10分)
由x2>1得f(x2)>f(2-x2),又f(x2)=0=f(x1),所以f(2-x2)<f(x1),
由g(x)=(2-x)ex在(-∞,1)上單調遞增,得f(x)=-g(x)+a在(-∞,1)單調遞減,
又2-x2<1,∴2-x2>x1,即x1+x2<2,得證.---------------------------------------(12分)】
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及轉化思想,是一道綜合題.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
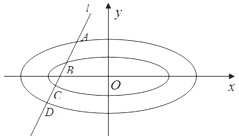 已知橢圓C1,C2均為中心在原點,焦點在x軸上的橢圓,離心率均為$\frac{{\sqrt{2}}}{2}$,其中C1的焦點坐標分別為(-1,0),(1,0),C2的左右頂點坐標為(-2,0),(2,0).
已知橢圓C1,C2均為中心在原點,焦點在x軸上的橢圓,離心率均為$\frac{{\sqrt{2}}}{2}$,其中C1的焦點坐標分別為(-1,0),(1,0),C2的左右頂點坐標為(-2,0),(2,0).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
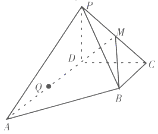 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠ADC=90°,Q為AD的中點,M是棱PC的中點,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠ADC=90°,Q為AD的中點,M是棱PC的中點,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4查看答案和解析>>
科目:高中數學 來源: 題型:填空題
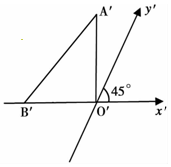 如圖所示,△A′O′B′表示水平放置△AOB的直觀圖,B′在x′軸上,A′O′和x′軸垂直,且A′O′=8,則△AOB的邊OB上的高為16$\sqrt{2}$.
如圖所示,△A′O′B′表示水平放置△AOB的直觀圖,B′在x′軸上,A′O′和x′軸垂直,且A′O′=8,則△AOB的邊OB上的高為16$\sqrt{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com