
【題目】在平面直角坐標系中,圓![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() .以
.以![]() 為頂點,
為頂點,![]() 分別為左、右焦點的橢圓
分別為左、右焦點的橢圓![]() ,恰好經過點
,恰好經過點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設經過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
【答案】(1) ![]() (2)當直線
(2)當直線![]() 的斜率為
的斜率為![]() 時,可使
時,可使![]() 的面積最大,其最大值
的面積最大,其最大值![]() .
.
【解析】試題分析:
(1)由已知可得,橢圓![]() 的焦點在
的焦點在![]() 軸上.設橢圓
軸上.設橢圓![]() 的標準方程為
的標準方程為![]() ,易知
,易知![]() ,結合橢圓過點
,結合橢圓過點![]() ,可得橢圓
,可得橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)由題意可知直線![]() 的斜率存在.設直線方程為
的斜率存在.設直線方程為![]() ,
,![]() .聯立直線方程與橢圓方程有
.聯立直線方程與橢圓方程有![]() .直線與橢圓交于不同的兩點,則
.直線與橢圓交于不同的兩點,則![]() ,
,![]() ,由弦長公式可得
,由弦長公式可得![]() ,而點
,而點![]() 到直線
到直線![]() 的距離
的距離![]() ,據此可得面積函數
,據此可得面積函數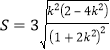 .換元令
.換元令![]() ,
,![]() ,結合二次函數的性質可得當直線
,結合二次函數的性質可得當直線![]() 的斜率為
的斜率為![]() 時,可使
時,可使![]() 的面積最大,其最大值
的面積最大,其最大值![]() .
.
試題解析:
(1)由已知可得,橢圓![]() 的焦點在
的焦點在![]() 軸上.
軸上.
設橢圓![]() 的標準方程為
的標準方程為![]() ,焦距為
,焦距為![]() ,則
,則![]() ,
,
∴![]() ,∴橢圓
,∴橢圓![]() 的標準方程為
的標準方程為![]() .
.
又∵橢圓![]() 過點
過點![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)由于點![]() 在橢圓
在橢圓![]() 外,所以直線
外,所以直線![]() 的斜率存在.
的斜率存在.
設直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() ,設
,設![]() .
.
由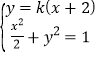 消去
消去![]() 得,
得,![]() .
.
由![]() 得
得![]() ,從而
,從而![]() ,
,
∴![]() .
.
∵點![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
∴![]() 的面積為
的面積為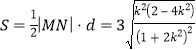 .
.
令![]() ,則
,則![]() ,
,
∴![]()
![]() ,
,
當![]() 即
即![]() 時,
時,![]() 有最大值,
有最大值,![]() ,此時
,此時![]() .
.
所以,當直線![]() 的斜率為
的斜率為![]() 時,可使
時,可使![]() 的面積最大,其最大值
的面積最大,其最大值![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案科目:高中數學 來源: 題型:
【題目】圓x2+y2-2y-1=0關于直線y=x對稱的圓的方程是 ( )
A. (x-1)2+y2=2 B. (x+1)2+y2=2 C. (x-1)2+y2=4 D. (x+1)2+y2=4
【答案】A
【解析】圓![]() 的標準方程為
的標準方程為![]() ,所以圓心為(0,1),半徑為
,所以圓心為(0,1),半徑為![]() ,圓心關于直線
,圓心關于直線![]() 的對稱點是(1,0),所以圓x2+y2-2y-1=0關于直線y=x對稱的圓的方程是
的對稱點是(1,0),所以圓x2+y2-2y-1=0關于直線y=x對稱的圓的方程是![]() ,選A.
,選A.
點睛:本題主要考查圓關于直線的對稱的圓的方程,屬于基礎題。解答本題的關鍵是求出圓心關于直線的對稱點,兩圓半徑相同。
【題型】單選題
【結束】
8
【題目】已知雙曲線的離心率為![]() ,焦點是
,焦點是![]() ,
, ![]() ,則雙曲線方程為 ( )
,則雙曲線方程為 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,橢圓
中,橢圓![]() 關于坐標軸對稱,以坐標原點
關于坐標軸對稱,以坐標原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系,
軸的正半軸為極軸建立極坐標系, ![]() ,
, ![]() 為橢圓
為橢圓![]() 上兩點.
上兩點.
(1)求直線![]() 的直角坐標方程與橢圓
的直角坐標方程與橢圓![]() 的參數方程;
的參數方程;
(2)若點![]() 在橢圓
在橢圓![]() 上,且點
上,且點![]() 在第一象限內,求四邊形
在第一象限內,求四邊形![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某中學舉行的物理知識競賽中,將三個年級參賽學生的成績在進行整理后分成5組,繪制出如圖所示的須率分布直方圖,圖中從左到右依次為第一、第二、第三、第四、第五小組.已知第三小組的頻數是15.

(1)求成績在50-70分的頻率是多少
(2)求這三個年級參賽學生的總人數是多少:
(3)求成績在80-100分的學生人數是多少
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的一段圖象如圖所示.
的一段圖象如圖所示.
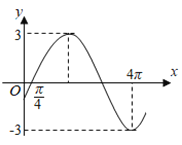
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的單調減區間,并指出
的單調減區間,并指出![]() 的最大值及取到最大值時
的最大值及取到最大值時![]() 的集合;
的集合;
(3)把![]() 的圖象向右至少平移多少個單位,才能使得到的圖象對應的函數為偶函數?
的圖象向右至少平移多少個單位,才能使得到的圖象對應的函數為偶函數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知線段AB的端點B的坐標為(3,0),端點A在圓![]() 上運動;
上運動;
(1)求線段AB中點M的軌跡方程;
(2)過點C(1,1)的直線m與M的軌跡交于G、H兩點,求以弦GH為直徑的圓的面積最小值及此時直線m的方程.
(3)若點C(1,1),且P在M軌跡上運動,求![]() 的取值范圍.(O為坐標原點)
的取值范圍.(O為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠利用隨機數表對生產的600個零件進行抽樣測試,先將600個零件進行編號,編號分別為001,002,![]() ,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若從表中第6行第6列開始向右依次讀取3個數據,則得到的第6個樣本編號![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過平面直角坐標系中的點P(4-3a,![]() )(a∈R)作圓x2+y2=1的兩條切線PA,PB,切點分別為A,B,則數量積
)(a∈R)作圓x2+y2=1的兩條切線PA,PB,切點分別為A,B,則數量積![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com