
(本小題滿分12分)
已知函數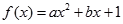 (
(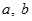 為實數,
為實數,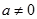 ,
,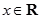 ),若
),若 ,且函數
,且函數 的值域為
的值域為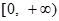 .
.
(1)求 的表達式;
的表達式;
(2)當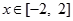 時,
時,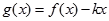 是單調函數,求實數
是單調函數,求實數 的取值范圍.
的取值范圍.
解:
(1)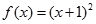 ;(2)
;(2)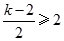 或
或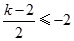 時
時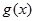 單調。
單調。
解析試題分析:(1)根據題意分析得到函數a,b的關系式, ,所以
,所以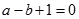 .,同時利用
.,同時利用 的值域為
的值域為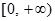 ,說明判別式為零。
,說明判別式為零。
(2)根據對稱軸和定義域的關系,來得到參數的范圍。
解:
(1)因為 ,所以
,所以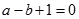 .
.
因為 的值域為
的值域為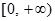 ,所以
,所以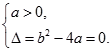 .................3分
.................3分
所以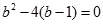 . 解得
. 解得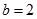 ,
,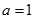 . 所以
. 所以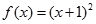 ....................6分
....................6分
(2)因為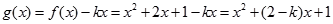
=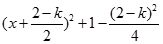 ,..................................8分
,..................................8分
所以當 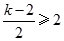 或
或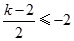 時
時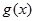 單調.................................12分
單調.................................12分
考點:本試題主要考查了二次函數解析式的求解,以及單調性的運用。
點評:解決該試題的關鍵是通過函數的值域,得到最小值為0,進而確定出判別式為零。那么再結合對稱軸和定義域的關系得到參數的范圍。


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數 (
( 為常數)。
為常數)。
(Ⅰ)函數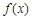 的圖象在點(
的圖象在點(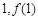 )處的切線與函數
)處的切線與函數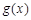 的圖象相切,求實數
的圖象相切,求實數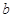 的值;
的值;
(Ⅱ)設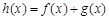 ,若函數
,若函數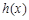 在定義域上存在單調減區間,求實數
在定義域上存在單調減區間,求實數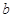 的取值范圍;
的取值范圍;
(Ⅲ)若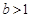 ,對于區間[1,2]內的任意兩個不相等的實數
,對于區間[1,2]內的任意兩個不相等的實數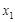 ,
,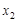 ,都有
,都有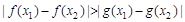 成立,求
成立,求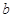 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
商店出售茶壺和茶杯,茶壺單價為每個20元,茶杯單價為每個5元,該店推出兩種促銷優惠辦法:
(1)買1個茶壺贈送1個茶杯;
(2)按總價打9.2折付款。
某顧客需要購買茶壺4個,茶杯若干個,(不少于4個),若設購買茶杯數為x個,付款數為y(元),試分別建立兩種優惠辦法中y與x之間的函數關系式,并討論該顧客買同樣多的茶杯時,兩種辦法哪一種更省錢?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠需要圍建一個面積為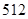 平方米的矩形堆料場,一邊可以利用原有的墻壁,其他三邊需要砌新的墻壁,問堆料場的長和寬各為多少時,才能使砌墻所用的材料最省?
平方米的矩形堆料場,一邊可以利用原有的墻壁,其他三邊需要砌新的墻壁,問堆料場的長和寬各為多少時,才能使砌墻所用的材料最省?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com