
 }滿足
}滿足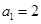 ,且點
,且點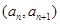 在函數(shù)
在函數(shù)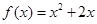 的圖象上,其中
的圖象上,其中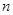 =1,2,3,….
=1,2,3,…. )}是等比數(shù)列;
)}是等比數(shù)列;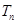 =(1+
=(1+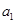 )(1+
)(1+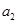 )…(1+
)…(1+ ),求
),求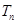 及數(shù)列{
及數(shù)列{ }的通項.
}的通項.  +1)=2n-1lg(1+
+1)=2n-1lg(1+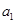 )
)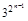 .∴
.∴ +1=
+1=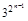 . 則
. 則  =
= 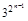 -1
-1 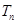 =(1+
=(1+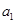 )(1+
)(1+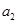 )…(1+
)…(1+ )=
)=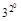 ·
·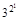 ·
·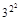 ·…·
·…·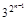
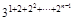 =
=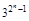 .∴
.∴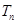 =
=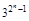 ,
, =
=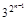 -1.
-1.  ,
,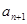 )在函數(shù)
)在函數(shù)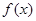 的圖象上,
的圖象上,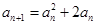 ,從而可得
,從而可得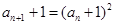 ,
,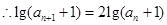 ,從而得到證明.
,從而得到證明.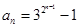 ,然后可知
,然后可知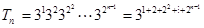 然后再利用等比數(shù)列前n項和公式求解.
然后再利用等比數(shù)列前n項和公式求解. ,
,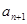 )在函數(shù)
)在函數(shù)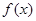 的圖象上,
的圖象上, 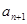 =
= +2
+2 ,∴
,∴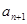 +1=
+1=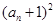 . …………4分
. …………4分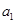 =2,∴
=2,∴ +1﹥1,∴l(xiāng)g(
+1﹥1,∴l(xiāng)g(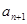 +1)=2lg(
+1)=2lg( +1).
+1). +1)}是公比為2的等比數(shù)列. …………6分
+1)}是公比為2的等比數(shù)列. …………6分 +1)=2n-1lg(1+
+1)=2n-1lg(1+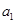 )
)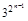 .∴
.∴ +1=
+1=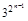 . 則
. 則  =
= 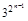 -1 …………9分
-1 …………9分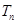 =(1+
=(1+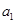 )(1+
)(1+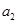 )…(1+
)…(1+ )=
)=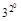 ·
·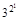 ·
·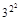 ·…·
·…·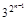
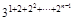 =
=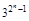 .∴
.∴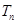 =
=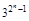 ,
, =
=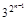 -1. …………12分
-1. …………12分

 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
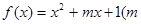 為整數(shù))且關(guān)于
為整數(shù))且關(guān)于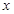 的方程
的方程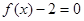 在區(qū)間
在區(qū)間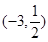 內(nèi)有兩個不同的實根,(1)求整數(shù)
內(nèi)有兩個不同的實根,(1)求整數(shù)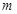 的值;(2)若對一切
的值;(2)若對一切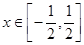 ,不等式
,不等式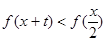 恒成立,求實數(shù)
恒成立,求實數(shù)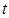 的取值范圍。
的取值范圍。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 ,那么廣告效應(yīng)D=a
,那么廣告效應(yīng)D=a -A,當(dāng)A=________時,取得最大值.
-A,當(dāng)A=________時,取得最大值.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com