
 ,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1-C2型點“
,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1-C2型點“ 內的點都不是“C1-C2型點”
內的點都不是“C1-C2型點”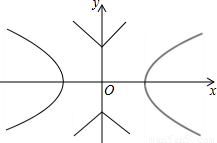
 ),當過左焦點的直線的斜率不存在時滿足左焦點是“C1-C2型點”,當斜率存在時,要保證斜率的絕對值大于等于該焦點與(0,1)連線的斜率;
),當過左焦點的直線的斜率不存在時滿足左焦點是“C1-C2型點”,當斜率存在時,要保證斜率的絕對值大于等于該焦點與(0,1)連線的斜率; 內的點且斜率為k的直線與C2無公共點,當|k|>1時,過圓
內的點且斜率為k的直線與C2無公共點,當|k|>1時,過圓 內的點且斜率為k的直線與C2有公共點,再由圓心到直線的距離小于半徑列式得出k的范圍,結果與|k|>1矛盾.從而證明了結論.
內的點且斜率為k的直線與C2有公共點,再由圓心到直線的距離小于半徑列式得出k的范圍,結果與|k|>1矛盾.從而證明了結論. ),寫出的直線方程可以是以下形式:
),寫出的直線方程可以是以下形式: 或
或 ,其中
,其中 .
. 有實數解,因此|kx|=|x|+1,得
有實數解,因此|kx|=|x|+1,得 .
. ,得
,得 ,矛盾.
,矛盾. ,取圓O內的一點Q,設有經過Q的直線l與C1,C2都有公共點,顯然l不與x軸垂直,
,取圓O內的一點Q,設有經過Q的直線l與C1,C2都有公共點,顯然l不與x軸垂直, 有實數解,
有實數解, ,
, ,從而
,從而 ,得k2<1,與|k|>1矛盾.
,得k2<1,與|k|>1矛盾. 內的點不是“C1-C2型點”.
內的點不是“C1-C2型點”.

 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:高中數學 來源: 題型:
 如圖,已知雙曲線C1:
如圖,已知雙曲線C1:| y2 |
| m |
| x2 |
| n |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•上海)如圖,已知雙曲線C1:
(2013•上海)如圖,已知雙曲線C1:| x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,已知雙曲線C1:![]() ,曲線C2:
,曲線C2:![]() .P是平面內一點.若存在過點P的直線與C1、C2都有共同點,則稱P為“C1-C2型點”.
.P是平面內一點.若存在過點P的直線與C1、C2都有共同點,則稱P為“C1-C2型點”.

(1)在正確證明C1的左焦點是“C1-C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線y=kx與C2有公共點,求證![]() >1,進而證明圓點不是“C1-C2型點”;
>1,進而證明圓點不是“C1-C2型點”;
(3)求證:圓![]() 內的點都不是“C1-C2型點”.
內的點都不是“C1-C2型點”.
查看答案和解析>>
科目:高中數學 來源:2013年全國普通高等學校招生統一考試文科數學(上海卷解析版) 題型:填空題
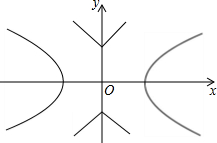
如圖,已知雙曲線C1: ,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“
,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“

(1)在正確證明C1的左焦點是“C1﹣C2型點“時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線y=kx與C2有公共點,求證|k|>1,進而證明原點不是“C1﹣C2型點”;
(3)求證:圓x2+y2= 內的點都不是“C1﹣C2型點”
內的點都不是“C1﹣C2型點”
查看答案和解析>>
科目:高中數學 來源:上海 題型:解答題
| x2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com