
對于平面直角坐標系內的任意兩點 ,定義它們之間的一種“距離”:
,定義它們之間的一種“距離”: .給出下列三個命題:
.給出下列三個命題:
①若點C在線段AB上,則 ;
;
②在 中,若∠C=90°,則
中,若∠C=90°,則 ;
;
③在 中,
中, .
.
其中真命題的個數為( )
A.0 B.1 C.2 D.3
B
【解析】
試題分析:①若點C在線段AB上,設點C(x0,y0)那么x0在x1,x2之間.y0在y1,y2之間,所以||AC||+||CB||=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=||AB||正確;
②平方后不能消除x0,y0,命題不成立;
③不妨假設C角為直角,以A為原點,AC所在直線為x軸,作直角坐標,得A(0 , 0 )、B(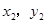 ),點C(
),點C(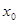 ,0)。代入③式中得 :︱
,0)。代入③式中得 :︱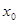 ︱+︱
︱+︱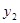 ︱=︱
︱=︱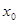 ︱+︱
︱+︱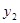 ︱,所以③不成立。故選B.
︱,所以③不成立。故選B.
考點:本題考查兩點間的距離公式。
點評:本題是新運算與絕對值的結合,應注意點C的不同位置。弄清新命題的運算規則,是本題的關鍵點;設出各點坐標,代入關系式計算,根據計算結果進行判斷是做本題的基本前提。


科目:高中數學 來源: 題型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中數學 來源:2014屆山東省濟寧市高二上學期期末理科數學(解析版) 題型:選擇題
對于平面直角坐標系內的任意兩點 ,定義它們之間的一種“距離”:
,定義它們之間的一種“距離”: 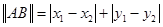 .給出下列三個命題:
.給出下列三個命題:
①若點C在線段AB上,則 ;
;
②在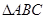 中,若∠C=90°,則
中,若∠C=90°,則 ;
;
③在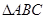 中,
中,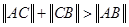 .
.
其中真命題的個數為( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年石景山區統一測試)對于平面直角坐標系內任意兩點![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() ),定義它們之間的一種“距離”:‖
),定義它們之間的一種“距離”:‖![]() ‖=
‖=![]() +
+![]() .給出下列三個命題:
.給出下列三個命題:
①若點C在線段AB上,則‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,則‖AC‖![]() +‖CB‖
+‖CB‖![]() =‖AB‖
=‖AB‖![]() ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命題的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
對于平面直角坐標系內的任意兩點![]() ,定義它們之間的一種“距離”:
,定義它們之間的一種“距離”:![]() .給出下列三個命題:
.給出下列三個命題:
①若點C在線段AB上,則![]() ;
;
②在![]() 中,若∠C=90°,則
中,若∠C=90°,則![]() ;
;
③在![]() 中,
中,![]() .
.
其中真命題的個數為( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com