
【題目】已知橢圓![]() 的一個頂點為拋物線
的一個頂點為拋物線![]() 的焦點,點
的焦點,點![]() 在橢圓
在橢圓![]() 上且
上且![]() ,
,![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,過
,過![]() 作
作![]() 的垂線交橢圓于另一點
的垂線交橢圓于另一點![]() ,連
,連![]() 交
交![]() 軸于
軸于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求證:![]() 軸;
軸;
(3)記![]() 的面積為
的面積為![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案科目:高中數學 來源: 題型:
【題目】每年10月中上旬是小麥的最佳種植時間,但小麥的發芽會受到土壤、氣候等多方面因素的影響.某科技小組為了解晝夜溫差的大小與小麥發芽的多少之間的關系,在不同的溫差下統計了100顆小麥種子的發芽數,得到了如下數據:
溫差 | 8 | 10 | 11 | 12 | 13 |
發芽數 | 79 | 81 | 85 | 86 | 90 |
(1)請根據統計的最后三組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由(1)中的線性回歸方程得到的估計值與前兩組數據的實際值誤差均不超過兩顆,則認為線性回歸方程是可靠的,試判斷(1)中得到的線性回歸方程是否可靠;
(3)若100顆小麥種子的發芽率為![]() 顆,則記為
顆,則記為![]() 的發芽率,當發芽率為
的發芽率,當發芽率為![]() 時,平均每畝地的收益為
時,平均每畝地的收益為![]() 元,某農場有土地10萬畝,小麥種植期間晝夜溫差大約為
元,某農場有土地10萬畝,小麥種植期間晝夜溫差大約為![]() ,根據(1)中得到的線性回歸方程估計該農場種植小麥所獲得的收益.
,根據(1)中得到的線性回歸方程估計該農場種植小麥所獲得的收益.
附:在線性回歸方程![]() 中,
中,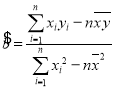 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
: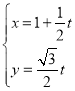 (
(![]() 為參數),曲線
為參數),曲線![]() :
:![]() (
(![]() 為參數).
為參數).
(1)設![]() 與
與![]() 相交于
相交于![]() 兩點,求
兩點,求![]() ;
;
(2)若把曲線![]() 上各點的橫坐標壓縮為原來的
上各點的橫坐標壓縮為原來的![]() 倍,縱坐標壓縮為原來的
倍,縱坐標壓縮為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點P是曲線
,設點P是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點![]() 作動直線
作動直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)當直線的斜率是![]() 時,
時,![]() ,求拋物線
,求拋物線![]() 的方程;
的方程;
(2)設![]() ,
,![]() 的中點是
的中點是![]() ,利用(1)中所求拋物線,試求點
,利用(1)中所求拋物線,試求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點為極點,
為參數),以原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為:
的極坐標方程為:![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 的極坐標方程,并指出它是何種曲線;
的極坐標方程,并指出它是何種曲線;
(Ⅱ)設![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com