
【題目】如圖,四邊形ABCD為矩形,沿AB將△ADC翻折成![]() .設(shè)二面角
.設(shè)二面角![]() 的平面角為
的平面角為![]() ,直線
,直線![]() 與直線BC所成角為
與直線BC所成角為![]() ,直線
,直線![]() 與平面ABC所成角為
與平面ABC所成角為![]() ,當(dāng)
,當(dāng)![]() 為銳角時(shí),有
為銳角時(shí),有

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
設(shè)三棱錐D-ABC是棱長(zhǎng)為2的正四面體,取AB中點(diǎn)E,DC中點(diǎn)M,AC中點(diǎn)M,連結(jié)DE、CE、MN、EN,過(guò)D作DO⊥CE,交CE于O,連結(jié)AO,則![]() ,
,![]() ,由此能求出結(jié)果.
,由此能求出結(jié)果.
設(shè)三棱錐D-ABC是棱長(zhǎng)為2的正四面體,
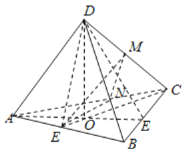
取AB中點(diǎn)E,DC中點(diǎn)M,AC中點(diǎn)M,連結(jié)DE、CE、MN、EN,過(guò)D作DO⊥CE,交CE于O,連結(jié)AO,則![]() ,
, ![]() ,DC=2,
,DC=2,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
取BC中點(diǎn)E,連結(jié)DE、AE,則DE⊥BC,AE⊥BC,
又![]() ,∴
,∴![]() 平面AED,∴
平面AED,∴![]() .
.
∴![]() .故選:B.
.故選:B.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量![]() 函數(shù)
函數(shù)![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)在![]() 中,角
中,角![]() 的對(duì)邊分別是
的對(duì)邊分別是![]() ,且滿足
,且滿足![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,(
,(![]() 為常數(shù)),
為常數(shù)),![]() .曲線
.曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與
處的切線與![]() 軸平行
軸平行
(1)求![]() 的值;
的值;
(2)求![]() 的單調(diào)區(qū)間和最小值;
的單調(diào)區(qū)間和最小值;
(3)若![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】要建造一段![]() 長(zhǎng)的高速公路,工程隊(duì)需要把380名施工人員分為兩組,一組負(fù)責(zé)
長(zhǎng)的高速公路,工程隊(duì)需要把380名施工人員分為兩組,一組負(fù)責(zé)![]() 的軟土地帶的施工,另一組完成剩下的
的軟土地帶的施工,另一組完成剩下的![]() 硬土地帶的施工.根據(jù)工程技術(shù)人員的測(cè)算,軟、硬地帶每米公路的工程量分別為50人·天和30人·天.
硬土地帶的施工.根據(jù)工程技術(shù)人員的測(cè)算,軟、硬地帶每米公路的工程量分別為50人·天和30人·天.
(1)設(shè)參與軟土地帶工作的人數(shù)為![]() 人,試分別寫出在軟、硬地帶筑路的時(shí)間
人,試分別寫出在軟、硬地帶筑路的時(shí)間![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(2)問(wèn)如何安排兩組的人數(shù),才能使全隊(duì)筑路工期最短?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() .
.
(Ⅰ)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() ,求
,求![]() 的解析式及其最小值(注:
的解析式及其最小值(注:![]() 為自然對(duì)數(shù)的底數(shù)).
為自然對(duì)數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】風(fēng)景秀美的寶湖畔有四棵高大的銀杏樹(shù),記作A,B,P,Q,湖岸部分地方圍有鐵絲網(wǎng)不能靠近.欲測(cè)量P,Q兩棵樹(shù)和A,P兩棵樹(shù)之間的距離,現(xiàn)可測(cè)得A,B兩點(diǎn)間的距離為100 m,∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,如圖所示.則P,Q兩棵樹(shù)和A,P兩棵樹(shù)之間的距離各為多少?

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若![]() 是
是![]() 的一個(gè)極值點(diǎn),求函數(shù)
的一個(gè)極值點(diǎn),求函數(shù)![]() 表達(dá)式, 并求出
表達(dá)式, 并求出![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() ,證明當(dāng)
,證明當(dāng)![]() 時(shí),
時(shí),![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的等腰梯形ABCD中,![]() ,
,![]() ,E為CD中點(diǎn).若沿AE將三角形DAE折起,并連接DB,DC,得到如圖所示的幾何體D-ABCE,在圖中解答以下問(wèn)題:
,E為CD中點(diǎn).若沿AE將三角形DAE折起,并連接DB,DC,得到如圖所示的幾何體D-ABCE,在圖中解答以下問(wèn)題:

(1)設(shè)G為AD中點(diǎn),求證:![]() 平面GBE;
平面GBE;
(2)若平面![]() 平面ABCE,且F為AB中點(diǎn),求證:
平面ABCE,且F為AB中點(diǎn),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 。
。
(I)當(dāng)![]() 時(shí),證明:當(dāng)
時(shí),證明:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(II)若當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求a的取值范圍。
恒成立,求a的取值范圍。
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com