【答案】
分析:(Ⅰ)用數學歸納法證明0<a
n<1,n∈N
*.(1)當n=1時,由已知得結論成立;(2)假設當n=k時,結論成立,即0<a
k<1.則當n=k+1時,因為0<x<1時,f′(x)=1-
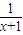
=
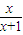
>0,所以f(x)在(0,1)上是增函數.可和f(0)<f(a
k)<f(1),即0<a
k+1<1<1-ln2<1.再由a
n+1-a
n=an-ln(1+a
n)-an=-ln(1+a
n)<0,有a
n+1<a
n.進而得到結論.
(Ⅱ)根據問題和a
n+1=f(a
n),可構造函數g(x)=
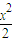
-f(x)=
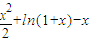
,0<x<1,即證g(x)>0成立,用導數法研究因為g′(x)=
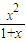
>0,知g(x)在(0,1)上增函數.得到結論.
(Ⅲ)由b
1=

,b
n+1≥

(n+1)b
n,可再由b
n>0,變形為
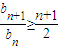
,從而由累乘法可得b
n=
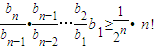
①,再由a
n+1<
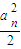
推知:
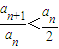
,再用累乘法可得
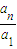
=
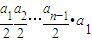
<
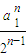
<
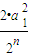
=
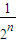
②.由①②兩式可得結論.
解答:解:(Ⅰ)先用數學歸納法證明0<a
n<1,n∈N
*.
(1)當n=1時,由已知得結論成立;
(2)假設當n=k時,結論成立,即0<a
k<1.則當n=k+1時,
∵0<x<1時,f′(x)=1-

=
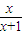
>0,
∴f(x)在(0,1)上是增函數.
又∵f(x)在[0,1]上連續,
∴f(0)<f(a
k)<f(1),即0<a
k+1<1<1-ln2<1.
故當n=k+1時,結論也成立.即0<a
n<1對于一切正整數都成立.(4分)
又由0<a
n<1,得a
n+1-a
n=an-ln(1+a
n)-an=-ln(1+a
n)<0,從而a
n+1<a
n.
綜上可知0<a
n+1<a
n<1(6分)
(Ⅱ)構造函數g(x)=

-f(x)=
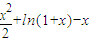
,0<x<1,
由g′(x)=
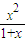
>0,知g(x)在(0,1)上增函數.
又g(x)在[0,1]上連續,
∴g(x)>g(0)=0.
∵0<a
n<1,
∴g(a
n)>0,即
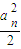
-f(an)>0,
從而a
n+1<
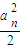
(10分)
(Ⅲ)∵b
1=

,b
n+1≥

(n+1)b
n,
∴b
n>0,
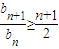
,
∴b
n=
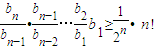
①,(12分)
由(Ⅱ)a
n+1<
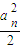
知:
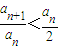
,
∴
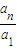
=
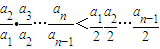
,
∵a
1=
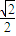
,n≥2,0<a
n+1<a
n<1
∴a
n<
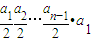
<
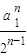
<
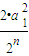
=
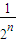
②.(14分)
由①②兩式可知:b
n>a
n•n!.(16分)
點評:本題主要考查數列與函數,不等式的綜合運用,主要涉及了數學歸納法,導數法,放縮法及累乘法等常用解題方法,綜合性強,難度大,要求思路要清,意志力要強.

 ,bn+1≥
,bn+1≥ (n+1)bn,n∈N*.求證:
(n+1)bn,n∈N*.求證: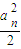
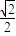 ,則當n≥2時,bn>an•n!.
,則當n≥2時,bn>an•n!.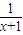 =
=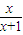 >0,所以f(x)在(0,1)上是增函數.可和f(0)<f(ak)<f(1),即0<ak+1<1<1-ln2<1.再由an+1-an=an-ln(1+an)-an=-ln(1+an)<0,有an+1<an.進而得到結論.
>0,所以f(x)在(0,1)上是增函數.可和f(0)<f(ak)<f(1),即0<ak+1<1<1-ln2<1.再由an+1-an=an-ln(1+an)-an=-ln(1+an)<0,有an+1<an.進而得到結論.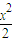 -f(x)=
-f(x)=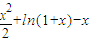 ,0<x<1,即證g(x)>0成立,用導數法研究因為g′(x)=
,0<x<1,即證g(x)>0成立,用導數法研究因為g′(x)=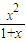 >0,知g(x)在(0,1)上增函數.得到結論.
>0,知g(x)在(0,1)上增函數.得到結論. ,bn+1≥
,bn+1≥ (n+1)bn,可再由bn>0,變形為
(n+1)bn,可再由bn>0,變形為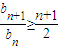 ,從而由累乘法可得bn=
,從而由累乘法可得bn=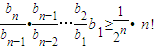 ①,再由an+1<
①,再由an+1<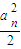 推知:
推知: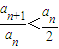 ,再用累乘法可得
,再用累乘法可得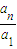 =
=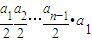 <
<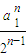 <
<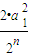 =
=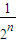 ②.由①②兩式可得結論.
②.由①②兩式可得結論. =
=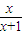 >0,
>0, -f(x)=
-f(x)=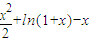 ,0<x<1,
,0<x<1,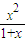 >0,知g(x)在(0,1)上增函數.
>0,知g(x)在(0,1)上增函數.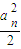 -f(an)>0,
-f(an)>0,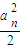 (10分)
(10分) ,bn+1≥
,bn+1≥ (n+1)bn,
(n+1)bn,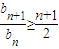 ,
,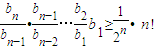 ①,(12分)
①,(12分)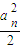 知:
知: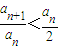 ,
,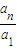 =
=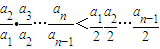 ,
,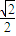 ,n≥2,0<an+1<an<1
,n≥2,0<an+1<an<1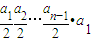 <
<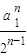 <
<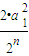 =
=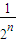 ②.(14分)
②.(14分)

 名師點撥卷系列答案
名師點撥卷系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<