
已知雙曲線![]() 的兩焦點為
的兩焦點為![]() ,
,![]() 為動點,若
為動點,若![]() .
.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 方程;
方程;
(Ⅱ)若![]() ,設直線過點
,設直線過點![]() ,且與軌跡
,且與軌跡![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 與
與![]() 交于點
交于點![]() .試問:當直線在變化時,點
.試問:當直線在變化時,點![]() 是否恒在一條定直線上?若是,請寫出這條定直線方程,并證明你的結論;若不是,請說明理由.
是否恒在一條定直線上?若是,請寫出這條定直線方程,并證明你的結論;若不是,請說明理由.
解法一:
(Ⅰ)由題意知:![]() ,又∵
,又∵![]() ,∴動點
,∴動點![]() 必在以
必在以![]() 為焦點,
為焦點,
長軸長為4的橢圓,∴![]() ,又∵
,又∵![]() ,
,![]() .
.
∴橢圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)由題意,可設直線為:![]() .
.
① 取![]() 得
得![]() ,直線
,直線![]() 的方程是
的方程是![]()
直線![]() 的方程是
的方程是![]() 交點為
交點為![]()
若![]() ,由對稱性可知交點為
,由對稱性可知交點為![]()
若點![]() 在同一條直線上,則直線只能為
在同一條直線上,則直線只能為![]() .
.
②以下證明對于任意的![]() 直線
直線![]() 與直線
與直線![]() 的交點
的交點![]() 均在直線
均在直線![]() 上.
上.
事實上,由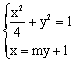 ,得
,得![]() 即
即![]() ,
,
記![]() ,則
,則![]() .
.
設![]() 與交于點
與交于點![]() 由
由![]() 得
得![]()
設![]() 與交于點
與交于點![]() 由
由![]() 得
得![]()
![]()
![]()
![]()
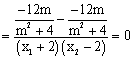 ,
,
∴![]() ,即
,即![]() 與
與![]() 重合,
重合,
這說明,當![]() 變化時,點
變化時,點![]() 恒在定直線
恒在定直線![]() 上.
上.
解法二:
(Ⅰ)同解法一.
(Ⅱ)取![]() 得
得![]() ,直線
,直線![]() 的方程是
的方程是![]() 直線
直線![]() 的方程是
的方程是![]() 交點為
交點為![]()
取![]() 得
得![]() ,直線
,直線![]() 的方程是
的方程是![]() 直線
直線![]() 的方程是
的方程是![]() 交點為
交點為![]() ∴若交點
∴若交點![]() 在同一條直線上,則直線只能為
在同一條直線上,則直線只能為![]() .
.
以下證明對于任意的![]() 直線
直線![]() 與直線
與直線![]() 的交點
的交點![]() 均在直線
均在直線![]() 上.
上.
事實上,由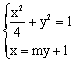 ,得
,得![]() 即
即![]() ,
,
記![]() ,則
,則![]() .
.
![]() 的方程是
的方程是![]()
![]() 的方程是
的方程是![]()
消去![]() 得
得![]() …………………………………… ①
…………………………………… ①
以下用分析法證明![]() 時,①式恒成立。
時,①式恒成立。
要證明①式恒成立,只需證明![]()
即證![]() 即證
即證![]() ……………… ②
……………… ②
∵![]() ∴②式恒成立.
∴②式恒成立.
這說明,當![]() 變化時,點
變化時,點![]() 恒在定直線
恒在定直線![]() 上.
上.
解法三:(Ⅰ)同解法一.(Ⅱ)由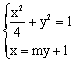 ,得
,得![]() 即
即![]() .
.
記![]() ,則
,則![]() .
.
![]() 的方程是
的方程是![]()
![]() 的方程是
的方程是![]()
由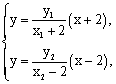 得
得![]()
即![]()
![]()
![]()
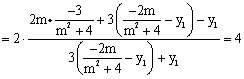 .
.
這說明,當![]() 變化時,點
變化時,點![]() 恒在定直線
恒在定直線![]() 上.
上.


科目:高中數學 來源:2011年上海市閔行區高考數學二模試卷(文科)(解析版) 題型:解答題
 的兩焦點為F、F',若該雙曲線與拋物線y2=8x有一個公共的焦點F,且兩曲線的一個
的兩焦點為F、F',若該雙曲線與拋物線y2=8x有一個公共的焦點F,且兩曲線的一個查看答案和解析>>
科目:高中數學 來源:2014屆浙江省高二上學期期末考試理科數學試卷(解析版) 題型:選擇題
已知雙曲線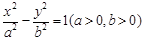 的兩焦點為
的兩焦點為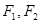 ,過
,過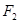 作
作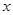 軸的垂線交雙曲線于
軸的垂線交雙曲線于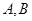 兩點,若
兩點,若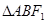 內切圓的半徑為
內切圓的半徑為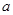 ,則此雙曲線的離心率為( )
,則此雙曲線的離心率為( )
A.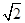 B.
B.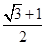 C.
C.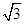 D.
D.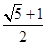
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河南省五市高三第二次聯考理科數學 題型:選擇題
已知雙曲線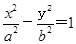 的兩焦點為F1、F2,點P在雙曲線上,∠F1PF2的平分線分線段F1F2的比為5 :1,則雙曲線離心率的取值范圍是
的兩焦點為F1、F2,點P在雙曲線上,∠F1PF2的平分線分線段F1F2的比為5 :1,則雙曲線離心率的取值范圍是
A.(1,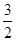 ]
B.(1,
]
B.(1,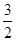 )
C.(2,
)
C.(2, 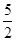 ] D.(
] D.(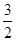 ,2]
,2]
查看答案和解析>>
科目:高中數學 來源:2010-2011年云南省高二上學期期末數學理卷 題型:解答題
(本題滿分12分)
已知雙曲線的兩焦點為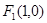 ,
,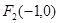 ,直線
,直線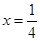 是雙曲線的一條準線,
是雙曲線的一條準線,
(Ⅰ)求該雙曲線的標準方程;
(Ⅱ)若點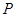 在雙曲線右支上,且
在雙曲線右支上,且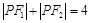 ,求
,求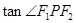 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com