
【題目】某企業生產甲、乙兩種產品均需用A,B兩種原料,已知每種產品各生產1噸所需原料及每天原料的可用限額如下表所示,如果生產1噸甲產品可獲利潤3萬元,生產1噸乙產品可獲利4萬元,則該企業每天可獲得最大利潤為萬元.
甲 | 乙 | 原料限額 | |
A(噸) | 3 | 2 | 12 |
B(噸) | 1 | 2 | 8 |
【答案】18
【解析】解:設每天生產甲乙兩種產品分別為x,y噸,利潤為z元, 則 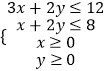 ,
,
目標函數為 z=3x+4y.
作出二元一次不等式組所表示的平面區域(陰影部分)即可行域.
由z=3x+4y得y=﹣ ![]() x+
x+ ![]() z,
z,
平移直線y=﹣ ![]() x+
x+ ![]() z
z
由圖象可知當直線y=﹣ ![]() x+
x+ ![]() z經過點B時,
z經過點B時,
直線y=﹣ ![]() x+
x+ ![]() z的截距最大,
z的截距最大,
此時z最大,
解方程組 ![]() ,解得x=2y=3,
,解得x=2y=3,
即B的坐標為(2,3),
∴zmax=3x+4y=6+12=18.
即每天生產甲乙兩種產品分別為2,3噸,能夠產生最大的利潤,最大的利潤是18萬元,
故答案為:18.
設每天生產甲乙兩種產品分別為x,y噸,利潤為z元,根據題目條件建立約束條件,
得到目標函數,畫出約束條件所表示的區域,再利用平移法求出z的最大值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】從某高中隨機選取5名高一男生,其身高和體重的數據如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
體重y(kg) | 63 | 66 | 70 | 72 | 74 |
根據如表可得回歸方程 ![]() =0.56x+
=0.56x+ ![]() ,據此模型可預報身高為172cm的高一男生的體重為( )
,據此模型可預報身高為172cm的高一男生的體重為( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是某縣參加2007年高考的學生身高條形統計圖,從左到右的各條形表示的學生人數依次記為A1 , A2 , …,A10(如A2表示身高(單位:cm)在[150,155)內的學生人數)圖2是統計圖1中身高在一定范圍內學生人數的一個算法流程圖.現要統計身高在160~180cm(含160cm,不含180cm)的學生人數,那么在流程圖中的判斷框內應填寫的條件是( ) 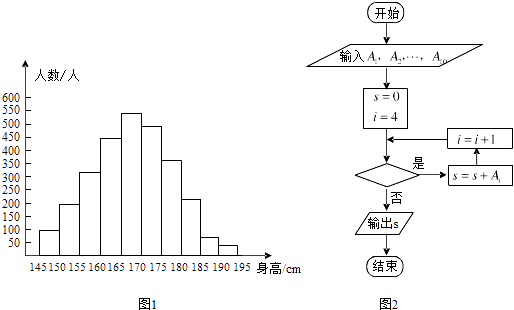
A.i<6
B.i<7
C.i<8
D.i<9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在x軸上,點 ![]() 在圓C上,圓心到直線2x﹣y=0的距離為
在圓C上,圓心到直線2x﹣y=0的距離為 ![]() ,則圓C的方程為( )
,則圓C的方程為( )
A.(x﹣2)2+y2=3
B.(x+2)2+y2=9
C.(x±2)2+y2=3
D.(x±2)2+y2=9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+|x﹣a|+1,x∈R,a∈R.
(Ⅰ)當a=1時,求函數f(x)的最小值;
(Ⅱ)若函數f(x)的最小值為g(a),令m=g(a),求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=logmx(m為常數,m>0且m≠1),設f(a1),f(a2),…,f(an)(n∈N+)是首項為4,公差為2的等差數列.
(Ⅰ)求證:數列logman=2n+2,{an}是等比數列;
(Ⅱ)若bn=anf(an),記數列{bn}的前n項和為Sn , 當m= ![]() 時,求Sn .
時,求Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB= ![]() ,BC=1,E為線段DC上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則K所形成軌跡的長度為( )
,BC=1,E為線段DC上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則K所形成軌跡的長度為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com