【題目】在△ABC中，內角A= 
，P為△ABC的外心，若 
=λ1 
+2λ2 
，其中λ1與λ2為實數，則λ1+λ2的最大值為（ ）
A.
B.1﹣ 
C.
D.1+ 
輕松暑假總復習系列答案科目：高中數學 來源： 題型：
【題目】已知雙曲線C的一個焦點與拋物線C1:y2=-16x的焦點重合,且其離心率為2.
(1)求雙曲線C的方程;
(2)求雙曲線C的漸近線與拋物線C1的準線所圍成三角形的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，不能證明AP⊥BC的條件是（ ） 
A.AP⊥PB，AP⊥PC
B.AP⊥PB，BC⊥PB
C.平面BPC⊥平面APC，BC⊥P C
D.AP⊥平面PBC
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，直三棱柱ABC-A1B1C1中，
且
，E是棱CC1中點，F是AB的中點.
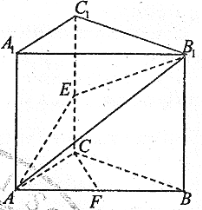
（1）求證：CF//平面AEB1；
（2）求點B到平面AEB1的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知四棱錐P-ABCD的底面ABCD是直角梯形,AB∥CD,AD⊥AB,AD=AB=
CD=1,PD⊥平面ABCD,PD=
,E是PC的中點.
(1)證明:BE∥平面PAD;
(2)求二面角E-BD-C的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某風景區水面游覽中心計劃國慶節當日投入之多3艘游船供游客觀光，過去10年的數據資料顯示每年國慶節當日客流量X（單位：萬人）都大于1，并把客流量分成三段整理得下表：
國慶節當日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
頻數 | 2 | 4 | 4 |
以這10年的數據資料記錄的隔斷客流量的頻率作為每年客流量在隔斷發生的概率，且每年國慶節當日客流量相互獨立．
（1）求未來連續3年國慶節當日中，恰好有1年國慶節當日客流量超過5萬人的概率；
（2）該水面游覽中心希望投入的游船盡可能使用，但每年國慶節當日游船最多使用量：（單位：艘）受當日客流量X（單位：萬人）的限制，其關聯關系如下表：
國慶節當日客流量X | 1＜X＜3 | 3≤X≤5 | X＞5 |
游船最多使用量 | 1 | 2 | 3 |
若某艘游船國慶節當日使用，則水面游覽中心國慶節當日可獲得利潤3萬元，若某艘游船國慶節當日不使用，則水面游覽中心國慶節當日虧損0.5萬元，記Y（單位：萬元）表示該水面游覽中心國慶節當日獲得總利潤，當Y的數學期望最大時稱水面游覽中心在國慶節當日效益最佳，問該水面游覽中心的國慶節當日應投入多少艘游船才能使該水面游覽中心在國慶節當日效益最佳？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個生產公司投資A生產線500萬元，每萬元可創造利潤
萬元，該公司通過引進先進技術，在生產線A投資減少了x萬元，且每萬元的利潤提高了
；若將少用的x萬元全部投入B生產線，每萬元創造的利潤為
萬元，其中
．
若技術改進后A生產線的利潤不低于原來A生產線的利潤，求x的取值范圍；
若生產線B的利潤始終不高于技術改進后生產線A的利潤，求a的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知隨機變量ξi滿足P（ξi=1）=pi ， P（ξi=0）=1﹣pi ， i=1，2．若0＜p1＜p2＜ 
，則（ ）
A.E（ξ1）＜E（ξ2），D（ξ1）＜D（ξ2）
B.E（ξ1）＜E（ξ2），D（ξ1）＞D（ξ2）
C.E（ξ1）＞E（ξ2），D（ξ1）＜D（ξ2）
D.E（ξ1）＞E（ξ2），D（ξ1）＞D（ξ2）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
