
(理科)(本小題滿分12分)
如圖,在五棱錐![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,
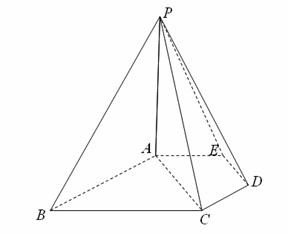
![]() ,三角形
,三角形![]() 是等腰三角形.
是等腰三角形.
(Ⅰ)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)求四棱錐![]() 的體積.
的體積.
(理科)(Ⅰ)證明:因?yàn)?sub>![]() ABC=45°,AB=2
ABC=45°,AB=2![]() ,BC=4,所以在
,BC=4,所以在![]() 中,由余弦定理得:
中,由余弦定理得:![]() ,解得
,解得![]() ,
,
所以![]() ,即
,即![]() ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥![]() ,
,
又PA![]() ,所以
,所以![]() ,又AB∥CD,所以
,又AB∥CD,所以![]() ,又因?yàn)?/p>
,又因?yàn)?/p>
![]() ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC內(nèi),過點(diǎn)A作![]() 于H,則
于H,則
![]() ,又AB∥CD,AB
,又AB∥CD,AB![]() 平面
平面![]() 內(nèi),所以AB平行于平面
內(nèi),所以AB平行于平面![]() ,所以點(diǎn)A到平面
,所以點(diǎn)A到平面![]() 的距離等于點(diǎn)B到平面
的距離等于點(diǎn)B到平面![]() 的距離,過點(diǎn)B作BO⊥平面
的距離,過點(diǎn)B作BO⊥平面![]() 于點(diǎn)O,則
于點(diǎn)O,則![]() 為所求角,且
為所求角,且![]() ,又容易求得
,又容易求得![]() ,所以
,所以![]() ,即
,即![]() =
=![]() ,所以直線PB與平面PCD所成角的大小為
,所以直線PB與平面PCD所成角的大小為![]() ;
;
(Ⅲ)由(Ⅰ)知![]() ,所以
,所以![]() ,又AC∥ED,所以四邊形ACDE是直角梯形,又容易求得,AC=
,又AC∥ED,所以四邊形ACDE是直角梯形,又容易求得,AC=![]() ,所以四邊形ACDE的面積為
,所以四邊形ACDE的面積為![]() ,所以四棱錐P—ACDE的體積為
,所以四棱錐P—ACDE的體積為![]() =
=![]() 。
。


 品學(xué)雙優(yōu)卷系列答案
品學(xué)雙優(yōu)卷系列答案 小學(xué)期末沖刺100分系列答案
小學(xué)期末沖刺100分系列答案 期末復(fù)習(xí)檢測(cè)系列答案
期末復(fù)習(xí)檢測(cè)系列答案 超能學(xué)典單元期中期末專題沖刺100分系列答案
超能學(xué)典單元期中期末專題沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西省高三4月月考數(shù)學(xué)文理合卷試卷(解析版) 題型:解答題
(理科)(本小題滿分12分)如圖分別是正三棱臺(tái)ABC-A1B1C1的直觀圖和正視圖,O,O1分別是上下底面的中心,E是BC中點(diǎn).
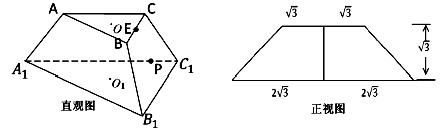
(1)求正三棱臺(tái)ABC-A1B1C1的體積;
(2)求平面EA1B1與平面A1B1C1的夾角的余弦;
(3)若P是棱A1C1上一點(diǎn),求CP+PB1的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西省高三4月月考數(shù)學(xué)文理合卷試卷(解析版) 題型:解答題
(理科)(本小題滿分12分)PM2.5是指懸浮在空氣中的空氣動(dòng)力學(xué)當(dāng)量直徑小于或等于2.5微米的顆粒物,也稱為可入肺顆粒物,根據(jù)現(xiàn)行國(guó)家標(biāo)準(zhǔn)GB3095 – 2012,PM2.5日均值在35微克/立方米以下空氣質(zhì)量為一級(jí);在35微克/立方米 ~ 75毫克/立方米之間空氣質(zhì)量為二級(jí);在75微克/立方米以上空氣質(zhì)量為超標(biāo)。從某自然保護(hù)區(qū)2012年全年每天的PM2.5監(jiān)測(cè)值數(shù)據(jù)中隨機(jī)地抽取10天的數(shù)據(jù)作為樣本,監(jiān)測(cè)值頻數(shù)如下表所示:
|
PM2.5日均值 (微克/立方米) |
[25,35] |
(35,45] |
(45,55] |
(55,65] |
(65,75] |
(75,85] |
|
頻數(shù) |
3 |
1 |
1 |
1 |
1 |
3 |
(1)從這10天的PM2.5日均值監(jiān)測(cè)數(shù)據(jù)中,隨機(jī)抽取3天,求恰有1天空氣質(zhì)量達(dá)到一級(jí)的概率;(2)從這10天的數(shù)據(jù)中任取3天數(shù)據(jù),記ξ表示抽到PM2.5監(jiān)測(cè)數(shù)據(jù)超標(biāo)的天數(shù),求ξ的分布列;(3)以這10天的PM2.5日均值來估計(jì)一年的空氣質(zhì)量狀況,則一年(按366天算)中平均有多少天的空氣質(zhì)量達(dá)到一級(jí)或二級(jí)。(精確到整數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(2012年高考福建卷理科19)(本小題滿分13分)
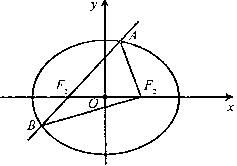 如圖,橢圓
如圖,橢圓![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,右焦點(diǎn)為
,右焦點(diǎn)為![]() ,離心率
,離心率![]() 。過
。過![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 的周長(zhǎng)為8。
的周長(zhǎng)為8。
(Ⅰ)求橢圓![]() 的方程。
的方程。
(Ⅱ)設(shè)動(dòng)直線![]() 與橢圓
與橢圓![]() 有且只有一個(gè)公共點(diǎn)
有且只有一個(gè)公共點(diǎn)![]() ,且與直線
,且與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() 。試探究:
。試探究:
在坐標(biāo)平面內(nèi)是否存在定點(diǎn)![]() ,使得以
,使得以![]() 為直徑的圓恒過點(diǎn)
為直徑的圓恒過點(diǎn)![]() ?若存在,求出點(diǎn)
?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,說明理由。
的坐標(biāo);若不存在,說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(2012年高考新課標(biāo)全國(guó)卷理科20)(本小題滿分12分)
設(shè)拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,準(zhǔn)線為
,準(zhǔn)線為![]() ,
,![]() ,已知以
,已知以![]() 為圓心,
為圓心,
![]() 為半徑的圓
為半徑的圓![]() 交
交![]() 于
于![]() 兩點(diǎn);
兩點(diǎn);
(1)若![]() ,
,![]() 的面積為
的面積為![]() ;求
;求![]() 的值及圓
的值及圓![]() 的方程;
的方程;
(2)若![]() 三點(diǎn)在同一直線
三點(diǎn)在同一直線![]() 上,直線
上,直線![]() 與
與![]() 平行,且
平行,且![]() 與
與![]() 只有一個(gè)公共點(diǎn),
只有一個(gè)公共點(diǎn),
求坐標(biāo)原點(diǎn)到![]() 距離的比值.
距離的比值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com