
已知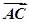 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
),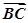 =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)設f(x)=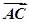 ·
·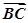 ,求f(x)的最小正周期和單調遞減區間;
,求f(x)的最小正周期和單調遞減區間;
(2)設有不相等的兩個實數x1,x2∈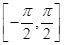 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
(1) T=2π
f(x)的單調遞減區間是[- +2kπ,
+2kπ,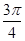 +2kπ](k∈Z)
+2kπ](k∈Z)
(2) x1+x2=-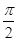
【解析】本試題主要是考查了向量的數量積公式以及三角函數的圖像與性質的綜合運用。注意解三角方程,要看范圍。
解:(1)由f(x)= ·
·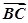 得
得
f(x)=(cos +sin
+sin )·(cos
)·(cos -sin
-sin )+(-sin
)+(-sin )·2cos
)·2cos
=cos2 -sin2
-sin2 -2sin
-2sin cos
cos =cosx-sinx=
=cosx-sinx= cos(x+
cos(x+ ),...........4分
),...........4分
所以f(x)的最小正周期T=2π.............6分
又由2kπ≤x+ ≤π+2kπ,k∈Z,
≤π+2kπ,k∈Z,
得- +2kπ≤x≤
+2kπ≤x≤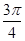 +2kπ,k∈Z.
+2kπ,k∈Z.
故f(x)的單調遞減區間是[- +2kπ,
+2kπ,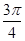 +2kπ](k∈Z) ……..8分
+2kπ](k∈Z) ……..8分
(2)由f(x)=1得 cos(x+
cos(x+ )=1,故cos(x+
)=1,故cos(x+ )=
)=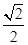 ……10分
……10分
又x∈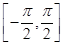 ,于是有x+
,于是有x+ ∈
∈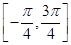 ,得x1=0,x2=-
,得x1=0,x2=-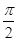 ,
,
所以x1+x2=-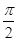


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:聊城一中高三數學測試——平面向量 題型:044
已知![]() =(cosα,sinα),
=(cosα,sinα),![]() =(cosβ,sinβ),且
=(cosβ,sinβ),且![]() 與
與![]() 之間滿足關系:
之間滿足關系:![]() ,其中k>0.
,其中k>0.
(Ⅰ)用k表示![]() ·
·![]() ;
;
(Ⅱ)求![]() ·
·![]() 的最小值,并求此時
的最小值,并求此時![]() 與
與![]() 夾角
夾角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知![]() =(cos+sin,-sin),
=(cos+sin,-sin),![]() =(cos-sin,2cos).
=(cos-sin,2cos).
(1)設f(x)=![]() ·
·![]() ,求f(x)的最小正周期和單調遞減區間;
,求f(x)的最小正周期和單調遞減區間;
(2)設有不相等的兩個實數x1,x2∈,且f(x1)=f(x2)=1,求x1+x2的值.
查看答案和解析>>
科目:高中數學 來源:2014屆河北衡水中學高一第二學期期末文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)
已知 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)設f(x)= ·
· ,求f(x)的最小正周期和單調遞減區間;
,求f(x)的最小正周期和單調遞減區間;
(2)設有不相等的兩個實數x1,x2∈ ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com