
分析 (1)根據導數的幾何意義分別求出函數f(x)與g(x)在x=4處的導數,根據函數f(x)和g(x)的圖象在x=5處的切線互相平行,建立等量關系,求出b即可;
(2)求導數,確定函數的單調性,即可求f(x)的極值.
解答 解:(1)g'(x)=$\frac{6}{{(x-4)}^{2}}$,∴g'(5)=6,
∵函數f(x)=x2+blnx和g(x)的圖象在x=5處的切線互相平行
∴f'(5)=6,
而f'(x)=2x+$\frac{b}{x}$,則f'(5)=10+$\frac{b}{5}$=6
∴b=-20;
(2)由(1)得:
f(x)=x2-20lnx,顯然f(x)的定義域為(0,+∞),
f'(x)=$\frac{{2x}^{2}-20}{x}$,令f'(x)=0,解得x=$\sqrt{10}$或x=-$\sqrt{10}$(舍去)
∴當0<x<$\sqrt{10}$時,f'(x)<0,當x>$\sqrt{10}$時,f'(x)>0
∴f(x)在(0,$\sqrt{10}$)上是單調遞減函數,在($\sqrt{10}$,+∞)上是單調遞增函數
∴f(x)在x=$\sqrt{10}$時取得極小值且極小值為f($\sqrt{10}$)=10-10ln10.
點評 本題主要考查了利用導數研究曲線上某點切線方程,以及兩條直線平行的判定等基礎題知識,考查運算求解能力、推理論證能力.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|-2<x<1} | B. | {x|-2<x<1或x>2} | C. | {x|x>2} | D. | {x|1<x<2或x<-2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
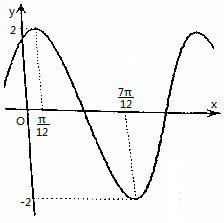 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一個周期內的圖象如圖.
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一個周期內的圖象如圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | ||
| C. | (3x)′=3x•log 3e | D. | (x2cos x)′=-2xsin x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 有最大值1 | B. | 圖象關于直線x=-$\frac{π}{6}$對稱 | ||
| C. | 在區間(-$\frac{π}{6}$,0)上單調遞增 | D. | 周期為π的偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在如圖所示的四棱錐P-ABCD中,四邊形ABCD為正方形,PA⊥CD,BC⊥平面PAB,且E、M、N分別為PD、CD、AD的中點,$\overrightarrow{PF}=3\overrightarrow{FD}$.
在如圖所示的四棱錐P-ABCD中,四邊形ABCD為正方形,PA⊥CD,BC⊥平面PAB,且E、M、N分別為PD、CD、AD的中點,$\overrightarrow{PF}=3\overrightarrow{FD}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com