【題目】已知動圓過定點
，且與定直線
相切.
（1）求動圓圓心的軌跡
的方程；
（2）若
是軌跡的動弦，且過， 分別以
、
為切點作軌跡的切線，設兩切線交點為
，證明:
.
【答案】（1）
（2）詳見解析
【解析】
試題（I）由題意可得：動圓圓心到定點（0，2）與到定直線y=-2的距離相等，利用拋物線的定義求軌跡方程即可；（II）設AB：y=kx+2，將直線的方程代入拋物線的方程，消去y得到關于x的一元二次方程，再結合根與系數的關系利用切線的幾何意義即可求得過拋物線上A、B兩點的切線斜率關系，從而解決問題
試題解析：（1）依題意，圓心的軌跡是以
為焦點，
為準線的拋物線
因為拋物線焦點到準線距離等于4, 所以圓心的軌跡方程是
（2）
， 
，
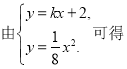
拋物線方程為
所以過拋物線上A、B兩點的切線斜率分別是
，
.
所以，
(注:也可設
,再由
,設
則直線AQ:
,聯立直線和拋物線方程,由直線和拋物線相切得
可得，同理可得，從而證
）
科目：高中數學 來源： 題型：
【題目】某高校為調查學生喜歡“應用統計”課程是否與性別有關，隨機抽取了選修課程的55名學生，得到數據如下表：
喜歡統計課程 | 不喜歡統計課程 | |
男生 | 20 | 5 |
女生 | 10 | 20 |
臨界值參考：
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式：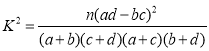
，其中
）
參照附表，得到的正確結論是（ ）
A.在犯錯誤的概率不超過
的前提下，認為“喜歡“應用統計”課程與性別有關”
B.在犯錯誤的概率不超過的前提下，認為“喜歡“應用統計”課程與性別無關”
C.有
以上的把握認為“喜歡應用統計”課程與性別有關”
D.有以上的把握認為“喜歡“應用統計”課程與性別無關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知過原點O的直線與函數
的圖象交于A，B兩點，分別過A，B作y軸的平行線與函數
圖象交于C，D兩點，若
軸，則四邊形ABCD的面積為_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在空間直角坐標系
中，已知正四棱錐
的高
，點
和
分別在
軸和
軸上，且
，點
是棱
的中點.
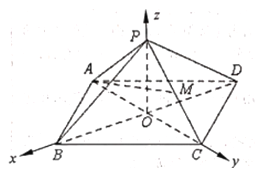
（1）求直線
與平面
所成角的正弦值；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司共有職工1500人,其中男職工1050人,女職工450人.為調查該公司職工每周平均上網的時間,采用分層抽樣的方法,收集了300名職工每周平均上網時間的樣本數據(單位:小時)
男職工 | 女職工 | 總計 | |
每周平均上網時間不超過4個小時 | |||
每周平均上網時間超過4個小時 | 70 | ||
總計 | 300 |
(Ⅰ)應收集多少名女職工樣本數據?
(Ⅱ)根據這300個樣本數據,得到職工每周平均上網時間的頻率分布直方圖(如圖所示),其中樣本數據分組區間為:
，
，
，
，
，
.試估計該公司職工每周平均上網時間超過4小時的概率是多少?
(Ⅲ)在樣本數據中,有70名女職工的每周平均上網時間超過4個小時.請將每周平均上網時間與性別的
列聯表補充完整,并判斷是否有95%的把握認為“該公司職工的每周平均上網時間與性別有關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（
）的左右焦點分別為
，
.橢圓C上任一點P都滿足
，并且該橢圓過點
.
（Ⅰ）求橢圓C的方程；
（Ⅱ）過點
的直線l與橢圓C交于A,B兩點，過點A作x軸的垂線，交該橢圓于點M，求證：
三點共線.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中正確的是（ ）
A.對具有線性相關關系的變量
有一組觀測數據
，其線性回歸方程是
，且
，則實數
的值是
B.正態分布
在區間
和
上取值的概率相等
C.若兩個隨機變量的線性相關性越強，則相關系數
的值越接近于1
D.若一組數據
的平均數是2，則這組數據的眾數和中位數都是2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
