
【題目】設函數f(x)在R上存在導數f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(6﹣m)﹣f(m)﹣18+6m≥0,則實數m的取值范圍為( )
A.[﹣3,3]
B.[3,+∞)
C.[2,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() .
.
(1)若直線![]() 與直線
與直線![]() 平行,求實數
平行,求實數![]() 的值;
的值;
(2)若![]() ,
, ![]() ,點
,點![]() 在直線
在直線![]() 上,已知
上,已知![]() 的中點在
的中點在![]() 軸上,求點
軸上,求點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)根據兩直線平行,對應方向向量共線,列方程即可求出![]() 的值;(2)根據
的值;(2)根據![]() 時,直線
時,直線![]() 的方程設出點
的方程設出點![]() 的坐標,由此求出
的坐標,由此求出![]() 的中點坐標,再由中點在
的中點坐標,再由中點在![]() 軸上求出點
軸上求出點![]() 的坐標.
的坐標.
試題解析:(1)∵直線![]() 與直線
與直線![]() 平行,
平行,
∴![]() ,
,
∴![]() ,經檢驗知,滿足題意.
,經檢驗知,滿足題意.
(2)由題意可知: ![]() ,
,
設![]() ,則
,則![]() 的中點為
的中點為![]() ,
,
∵![]() 的中點在
的中點在![]() 軸上,∴
軸上,∴![]() ,
,
∴![]() .
.
【題型】解答題
【結束】
16
【題目】在平面直角坐標系xOy中,已知△ABC三個頂點坐標為A(7,8),B(10,4),C(2,-4).
(1)求BC邊上的中線所在直線的方程;
(2)求BC邊上的高所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某社區中學生的課外活動,對該社區的100名中學生進行了調研,隨機抽取了若干名,年齡全部介于13與18之間,將年齡按如下方式分成五組:第一組![]() ;第二組
;第二組![]() ;第五組
;第五組![]() .按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三個組的頻率之比為
.按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三個組的頻率之比為![]() ,且第二組的頻數為4.
,且第二組的頻數為4.
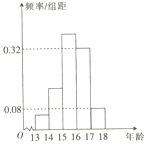
(1)試估計這100名中學生中年齡在![]() 內的人數;
內的人數;
(2)求調研中隨機抽取的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρ2(1+3sin2θ)=4,曲線C2: ![]() (θ為參數).
(θ為參數).
(Ⅰ)求曲線C1的直角坐標方程和C2的普通方程;
(Ⅱ)極坐標系中兩點A(ρ1 , θ0),B(ρ2 , θ0+ ![]() )都在曲線C1上,求
)都在曲線C1上,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準 ![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過 ![]() 的部分按平價收費,超出
的部分按平價收費,超出 ![]() 的部分按議價收費,為了了解居民用水情況,通過抽祥,獲得了某年100位居民毎人的月均用水量(單位:噸),將數據按照
的部分按議價收費,為了了解居民用水情況,通過抽祥,獲得了某年100位居民毎人的月均用水量(單位:噸),將數據按照 ![]() 分成
分成 ![]() 組,制成了如圖所示的頻率分布直方圖.
組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖中a的值;
(2)若該市有110萬居民,估計全市居民中月均用水量不低于 ![]() 噸的人數,并說明理由;
噸的人數,并說明理由;
(3)若該市政府希望使80%的居民每月的用水量不超過標準 ![]() (噸),估計x的值(精確到0.01),并說明理由.
(噸),估計x的值(精確到0.01),并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=cos(2x+ ![]() )+2cos2x,x∈R.
)+2cos2x,x∈R.
(1)求函數f(x)的最小正周期和單調增區間;
(2)將函數f(x)的圖象向右平移 ![]() 個單位長度后得到函數g(x)的圖象,求函數g(x)在區間
個單位長度后得到函數g(x)的圖象,求函數g(x)在區間 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線x2=4y的焦點F的直線l與拋物線相交于A、B兩點. 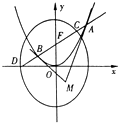
(1)設拋物線在A、B處的切線的交點為M,若點M的橫坐標為2,求△ABM的外接圓方程.
(2)若直線l與橢圓 ![]() +
+ ![]() =1的交點為C,D,問是否存在這樣的直線l使|AF||CF|=|BF||DF|,若存在,求出l的方程;若不存在,說明理由.
=1的交點為C,D,問是否存在這樣的直線l使|AF||CF|=|BF||DF|,若存在,求出l的方程;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com