
(2006
北京朝陽模擬)如圖所示,已知圓 ,設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.
,設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.
(1)
當r=2時,求滿足條件的P點的坐標;(2)
當r (1,+∞)時,求點N的軌跡G的方程;
(1,+∞)時,求點N的軌跡G的方程;
(3)
過點P(0,2)的直線l與(2)中軌跡G相交于兩個不同的點E、F,若 ,求直線l的斜率的取值范圍.
,求直線l的斜率的取值范圍.

|
解析: (1)解法一:由已知得,r=2時,可求得M點的坐標為M(-1,0).設 P(0,b),則由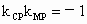 . .
( 或用勾股定理)得 . .
∴ b=±1,即點P坐標為(0,±1).解法二:同上可得 M(-1,0)設N(x,y),則
解得 N(1,±2).∴ MN的中點P坐標為(0,±1),(2) 解法一:設N(x,y),由已知得,在圓方程中令 y=0,求得M點的坐標為(1-r,0).設 P(0,b),則由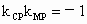 . .
( 或用 ) )
∵點 P為線段MN的中點,∴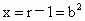 ,y=2b.又r>1, ,y=2b.又r>1,
∴點 N的軌跡方程為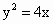 (x≠0). (x≠0).
解法二:設 N(x,y),同上可得 M(1-r,0),則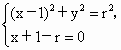 ,消去r,又r>1, ,消去r,又r>1,
∴點 N的軌跡方程為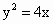 (x≠0). (x≠0).
(3) 依題意得直線l的斜率存在且不為0,設直線l的方程為y=kx+2,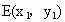 , ,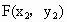 , ,
由  ,得 ,得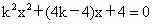 . .
由Δ =-32k+16>0,得 . .
∵  , ,
∴ 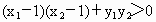 . .
∴ 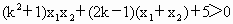 . .
得 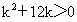 . .
∴ k>0或k<-12.∴ 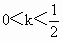 或k<-12. 或k<-12. |


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:013
(2006
北京朝陽模擬)將直線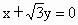 繞原點按順時針方向旋轉30°,所得直線與圓
繞原點按順時針方向旋轉30°,所得直線與圓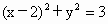 的位置關系是
的位置關系是
[
]A
.直線與圓相離B
.直線與圓相交但不過圓心C
.直線與圓相切D
.直線過圓心查看答案和解析>>
科目:高中數學 來源: 題型:044
(2006
北京朝陽模擬)已知函數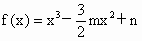 ,1<m<2.
,1<m<2.
(1)
若f(x)在區間[-1,1]上的最大值為1,最小值為-2,求m、n的值;(2)
在(1)條件下,求經過點P(2,1)且與曲線f(x)相切的直線l的方程;(3)
設函數f(x)的導函數為g(x),函數 ,試判斷函數F(x)的極值點個數,并求出相應實數m的范圍.
,試判斷函數F(x)的極值點個數,并求出相應實數m的范圍.查看答案和解析>>
科目:高中數學 來源: 題型:013
(2006
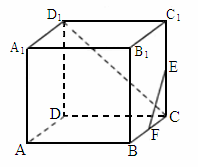
北京朝陽模擬)如下圖,正方體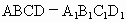 中,E、F分別是棱
中,E、F分別是棱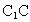 與BC的中點,則直線EF與直線
與BC的中點,則直線EF與直線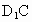 所成角的大小是
所成角的大小是
[
]|
A .45° |
B .60° |
|
C .75° |
D .90° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com