分析：先寫出兩角差的余弦公式，再以坐標原點為中心作單位圓，以Ox為始邊作α、β，它們的終邊分別與單位圓相交于點P，Q，利用向量的數量積公式可得結論．
解答：兩角差的余弦公式：cos（α-β）=cosαcosβ+sinαsinβ，證明如下：
以坐標原點為中心作單位圓，以Ox為始邊作α、β，它們的終邊分別與單位圓相交于點P，Q，則P（cosα，sinα），Q（cosβ，sinβ），|
|=|
|=1
∵α-β=
＜，＞+2kπ，k∈Z（左圖），或β-α=
＜，＞+2kπ，k∈Z（右圖），
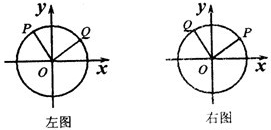
∴cos（α-β）=cos
＜，＞=
||||cos＜，＞=
•=（cosα，sinα）•（cosβ，sinβ）=cosαcosβ+sinαsinβ
點評：本題考查兩角差的余弦公式，考查向量的數量積，考查學生的計算能力，屬于基礎題．
名校課堂系列答案