
【題目】已知圓![]() 的標準方程為
的標準方程為![]() ,圓心為
,圓心為![]() ,直線
,直線![]() 的方程為
的方程為![]() ,點
,點![]() 在直線
在直線![]() 上,過
上,過![]() 點作圓
點作圓![]() 的切線
的切線![]() ,
,![]() ,切點分別為
,切點分別為![]() ,
,![]() .
.
(1)若![]() ,試求點
,試求點![]() 的坐標;
的坐標;
(2)若![]() 點的坐標為
點的坐標為![]() ,過
,過![]() 作直線與圓
作直線與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(3)求證:經過![]() ,
,![]() ,
,![]() 三點的圓必過定點,并求出所有定點的坐標.
三點的圓必過定點,并求出所有定點的坐標.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
試題(1)點![]() 在直線
在直線![]() 上,設
上,設![]() ,由對稱性可知
,由對稱性可知![]() ,可得
,可得![]() ,從而可得點
,從而可得點![]() 坐標.(2)分析可知直線
坐標.(2)分析可知直線![]() 的斜率一定存在,設其方程為:
的斜率一定存在,設其方程為:![]() .由已知分析可得圓心到直線
.由已知分析可得圓心到直線![]() 的距離為
的距離為![]() ,由點到線的距離公式可求得
,由點到線的距離公式可求得![]() 的值.(3)由題意知
的值.(3)由題意知![]() ,即
,即![]() .所以過
.所以過![]() 三點的圓必以
三點的圓必以![]() 為直徑.設
為直徑.設![]() ,從而可得圓的方程,根據
,從而可得圓的方程,根據![]() 的任意性可求得此圓所過定點.
的任意性可求得此圓所過定點.
試題解析:解:(1)直線![]() 的方程為
的方程為![]() ,點
,點![]() 在直線
在直線![]() 上,設
上,設![]() ,
,
由題可知![]() ,所以
,所以![]() ,
,
解之得:![]() 故所求點
故所求點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
(2)易知直線![]() 的斜率一定存在,設其方程為:
的斜率一定存在,設其方程為:![]() ,
,
由題知圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,所以
,所以![]() ,
,
解得,![]() 或
或![]() ,
,
故所求直線![]() 的方程為:
的方程為:![]() 或
或![]() .
.
(3)設![]() ,則
,則![]() 的中點
的中點![]() ,因為
,因為![]() 是圓
是圓![]() 的切線,
的切線,
所以經過![]() 三點的圓是以
三點的圓是以![]() 為圓心,以
為圓心,以![]() 為半徑的圓,
為半徑的圓,
故其方程為:![]()
化簡得:![]() ,此式是關于
,此式是關于![]() 的恒等式,
的恒等式,
故![]() 解得
解得![]() 或
或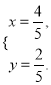
所以經過![]() 三點的圓必過定點
三點的圓必過定點![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】給出下列命題:
①![]() ,不等式
,不等式![]() 恒成立;
恒成立;
②若![]() ,則
,則![]() ;
;
③“若![]() 且
且![]() ,則
,則![]() ”的逆否命題;
”的逆否命題;
④若命題![]() ,命題
,命題![]() ,則命題
,則命題![]() 是真命題.
是真命題.
其中,真命題為( )
A.①③④B.①②C.①②③D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①“數列![]() 為等比數列”是“數列
為等比數列”是“數列![]() 為等比數列”的充分不必要條件;
為等比數列”的充分不必要條件;
②“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 上為增函數”的充要條件;
上為增函數”的充要條件;
③“![]() ”是“直線
”是“直線![]() 與直線
與直線![]() 互相垂直”的充要條件;
互相垂直”的充要條件;
④設![]() ,
,![]() ,
,![]() 分別是
分別是![]() 三個內角
三個內角![]() ,
,![]() ,
,![]() 所對的邊,若
所對的邊,若![]() ,
,![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要不充分條件.其中,真命題的序號是________.
”的必要不充分條件.其中,真命題的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() =(2sin x,
=(2sin x,![]() cos x),
cos x),![]() =(-sin x,2sin x),函數f(x)=
=(-sin x,2sin x),函數f(x)=![]() ·
·![]()
(1)求f(x)的單調遞增區間;
(2)在△ABC中,a,b,c分別是角A,B,C的對邊,且f(C)=1,c=1,ab=2![]() ,且a>b,求a,b的值.
,且a>b,求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,隨著中國第一款5G手機投入市場,5G技術已經進入高速發展階段.已知某5G手機生產廠家通過數據分析,得到如下規律:每生產手機![]() 萬臺,其總成本為
萬臺,其總成本為![]() ,其中固定成本為800萬元,并且每生產1萬臺的生產成本為1000萬元(總成本=固定成本+生產成本),銷售收入
,其中固定成本為800萬元,并且每生產1萬臺的生產成本為1000萬元(總成本=固定成本+生產成本),銷售收入![]() 萬元滿足
萬元滿足
(1)將利潤![]() 表示為產量
表示為產量![]() 萬臺的函數;
萬臺的函數;
(2)當產量![]() 為何值時,公司所獲利潤最大?最大利潤為多少萬元?
為何值時,公司所獲利潤最大?最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 同時滿足:①對于任意的正整數
同時滿足:①對于任意的正整數![]() ,
, ![]() 恒成立;②對于給定的正整數
恒成立;②對于給定的正整數![]() ,
, ![]() 對于任意的正整數
對于任意的正整數![]() 恒成立,則稱數列
恒成立,則稱數列![]() 是“
是“![]() 數列”.
數列”.
(1)已知![]() 判斷數列
判斷數列![]() 是否為“
是否為“![]() 數列”,并說明理由;
數列”,并說明理由;
(2)已知數列![]() 是“
是“![]() 數列”,且存在整數
數列”,且存在整數![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差數列,證明:
成等差數列,證明: ![]() 是等差數列.
是等差數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com