
【題目】甲、乙兩家物流公司都需要進行貨物中轉,由于業務量擴大,現向社會招聘貨車司機,其日工資方案如下:甲公司,底薪80元,司機毎中轉一車貨物另計4元:乙公司無底薪,中轉40車貨物以內(含40車)的部分司機每車計6元,超出40車的部分司機每車計7元.假設同一物流公司的司機一填中轉車數相同,現從這兩家公司各隨機選取一名貨車司機,并分別記錄其50天的中轉車數,得到如下頻數表:
甲公司送餐員送餐單數頻數表
送餐單數 | 38 | 39 | 40 | 41 | 42 |
天數 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐員送餐單數頻數表
送餐單數 | 38 | 39 | 40 | 41 | 42 |
天數 | 5 | 10 | 10 | 20 | 5 |
(1)現從記錄甲公司的50天貨物中轉車數中隨機抽取3天的中轉車數,求這3天中轉車數都不小于40的概率;
(2)若將頻率視為概率,回答下列兩個問題:
①記乙公司貨車司機日工資為X(單位:元),求X的分布列和數學期望E(X);
②小王打算到甲、乙兩家物流公司中的一家應聘,如果僅從日工資的角度考慮,請利用所學的統計學知識為小王作出選擇,并說明理由.
【答案】(1)![]() ;(2)①見解析,②若從日工資的角度考慮,小王應該選擇乙公司
;(2)①見解析,②若從日工資的角度考慮,小王應該選擇乙公司
【解析】
(1)根據古典概型概率公式以及組合數求結果,(2)①先確定隨機變量,再分別求對應概率,最后根據數學期望公式得期望,②先求甲公司日工資數學期望,再與①期望比較大小即得結果
(1)設“這三天中轉車數都不小于40”的事件為A,則P(A)=![]() =
=![]() .
.
(2)①設乙公司貨車司機中轉貨車數為t,則X=![]() ,
,
則X的所有取值分別為228,234,240,247,254,其分布列為:
日工資 | 228 | 234 | 240 | 247 | 254 |
概率P |
|
|
|
|
|
∴E(X)=228×![]() +234×
+234×![]() +240×
+240×![]() +247×
+247×![]() +254×
+254×![]() =241.8.
=241.8.
②設公司貨車司機日工資為Y,日中轉車數為μ,則Y=4μ+80,
則Y的所有可能取值為232,236,240,244,248,則分布列為:
日工資 | 232 | 236 | 240 | 244 | 248 |
概率P |
|
|
|
|
|
E(Y)=![]() +248×
+248×![]() =238.8.
=238.8.
由E(X)>E(Y),知:若從日工資的角度考慮,小王應該選擇乙公司.


科目:高中數學 來源: 題型:
【題目】隨著手機的發展,“微信”逐漸成為人們交流的一種形式,某機構對“使用微信交流”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信交流”贊成人數如表:
年齡(單位:歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年齡55歲為分界點”,由以上統計數據完成下面![]() 列聯表,并判斷是否有99.9%的把握認為“使用微信交流”的態度與人的年齡有關;
列聯表,并判斷是否有99.9%的把握認為“使用微信交流”的態度與人的年齡有關;
年齡不低于55歲的人數于 | 年齡低于55歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(2)若從年齡在![]() 的被調查人中隨機選取2人進行追蹤調查,求2人中至少有1人贊成“使用微信交流”的概率.
的被調查人中隨機選取2人進行追蹤調查,求2人中至少有1人贊成“使用微信交流”的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且與
且與![]() 軸不重合,交圓
軸不重合,交圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
(1)求![]() 的值;
的值;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,與直線
兩點,與直線![]() 相交于
相交于![]() 點,試問在橢圓
點,試問在橢圓![]() 上是否存在一定點
上是否存在一定點![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差數列(其中
成等差數列(其中![]() ,
,![]() ,
,![]() 分別指直線
分別指直線![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,2012年春節,攝影愛好者S在某公園A處,發現正前方B處有一立柱,測得立柱頂端O的仰角和立柱底部B的俯角均為![]() ,已知S的身高約為
,已知S的身高約為![]() 米(將眼睛距地面的距離按
米(將眼睛距地面的距離按![]() 米處理)
米處理)
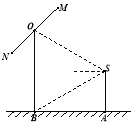
(1) 求攝影者到立柱的水平距離和立柱的高度;
(2) 立柱的頂端有一長2米的彩桿MN繞中點O在S與立柱所在的平面內旋轉.攝影者有一視角范圍為![]() 的鏡頭,在彩桿轉動的任意時刻,攝影者是否都可以將彩桿全部攝入畫面?說明理由.
的鏡頭,在彩桿轉動的任意時刻,攝影者是否都可以將彩桿全部攝入畫面?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 1左右焦點為F1,F2直線(
1左右焦點為F1,F2直線(![]() 1)x
1)x![]() y
y![]() 0與該橢圓有一個公共點在y軸上,另一個公共點的坐標為(m,1).
0與該橢圓有一個公共點在y軸上,另一個公共點的坐標為(m,1).
(1)求橢圓C的方程;
(2)設P為橢圓C上任一點,過焦點F1,F2的弦分別為PM,PN,設![]() λ1
λ1![]() λ2
λ2![]() ,求λ1+λ2的值.
,求λ1+λ2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A為焦距為![]() 的橢圓E:
的橢圓E:![]() (a>b>0)的右頂點,點P(0,
(a>b>0)的右頂點,點P(0,![]() ),直線PA交橢圓E于點B,
),直線PA交橢圓E于點B,![]() .
.
(1)求橢圓E的方程;
(2)設過點P且斜率為![]() 的直線
的直線![]() 與橢圓E交于M、N兩點(M在P、N之間),若四邊形MNAB的面積是△PMB面積的5倍.求直線
與橢圓E交于M、N兩點(M在P、N之間),若四邊形MNAB的面積是△PMB面積的5倍.求直線![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(卷號)2040818101747712
(題號)2050752239689728
(題文)
在平面直角坐標系中,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系.已知直線![]() 的參數方程為
的參數方程為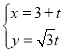 (
(![]() 為參數),曲線C的極坐標方程為
為參數),曲線C的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為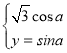 ,(a為參數)。以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C2的極坐標方程為
,(a為參數)。以坐標原點為極點,以x軸的正半軸為極軸,建立極坐標系,曲線C2的極坐標方程為![]() ,將C2逆時針旋轉
,將C2逆時針旋轉![]() 以后得到曲線C3.
以后得到曲線C3.
(1)寫出C1與C3的極坐標方程;
(2)設C2與C3分別交曲線C1于A、B和C、D四點,求四邊形ACBD面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com