
| A. | 4 | B. | $\frac{13}{4}$ | C. | 26 | D. | 52 |
分析 利用題中條件:“f(x)•f(x+2)=13”得出函數f(x)是周期函數,從而利用f(3)的值求出f(22017)即可
解答 解:∵f(x)•f(x+2)=13
∴f(x+2)•f(x+4)=13,
∴f(x+4)=f(x),
∴f(x)是一個周期為4的周期函數,
∴f(22017)=f(4×5504+1)=f(1)=$\frac{13}{f(3)}$=$\frac{13}{4}$.
故選:B.
點評 本題主要考查了抽象函數及其應用,考查分析問題和解決問題的能力,屬于中檔題.函數的周期性是高考函數題的重點考查內容,幾個重要的周期公式要熟悉,如:(1)f(x+a)=f(x-a),則T=2a;(2)f(x+a)=-$\frac{1}{f(x)}$,則T=2a等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | x1>x2 | B. | |x1|<|x2| | C. | x1>|x2| | D. | x12>x22 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
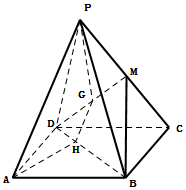 如圖,已知四邊形ABCD是平行四邊形,點P是平面ABCD外一點,M是PC的中點,在DM上取一點G,過G和AP作平面交平面BDM于GH.求證:
如圖,已知四邊形ABCD是平行四邊形,點P是平面ABCD外一點,M是PC的中點,在DM上取一點G,過G和AP作平面交平面BDM于GH.求證:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com