

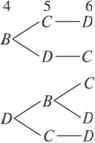
解析:本小題是一道較難的排列題,主要考查分類計數及分步計數原理,注重了綜合性與應用性.
先種1、2、3、4四個部分,分成四類:
第一類是這四部分顏色各不相同,共有![]() =24種不同的種數,此時需再考慮第5部分,必與2、3之一顏色相同,若相同,則第6部分有2種不同的種法;若5、3相同,則第6部分只有1種種法.故共有24×(1×2+1×1)=72種不同的種法.
=24種不同的種數,此時需再考慮第5部分,必與2、3之一顏色相同,若相同,則第6部分有2種不同的種法;若5、3相同,則第6部分只有1種種法.故共有24×(1×2+1×1)=72種不同的種法.
第二類是這四部分顏色有相同之處,此時只有2、4部分顏色相同,共有A34=24種不同的種法,這時第5部分分為2種不同的種法(可與3同也可選剩余的另一種顏色),第6部分只有一種種法.共有24×2×1=48種不同的種法.
所以總的方法數為72+48=120種.
答案:120


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
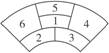
 15、某城市在中心廣場建造一個花圃,花圃分為6個部分(如圖).現要栽種4種不同顏色的花,每部分栽種一種且相鄰部分不能栽種同樣顏色的花,不同的栽種方法有
15、某城市在中心廣場建造一個花圃,花圃分為6個部分(如圖).現要栽種4種不同顏色的花,每部分栽種一種且相鄰部分不能栽種同樣顏色的花,不同的栽種方法有
查看答案和解析>>
科目:高中數學 來源: 題型:
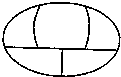 某城市在中心廣場建造一個花圃(如圖),花圃分為5個部分,現要將4種顏色的花全部種在花圃中,每部分種一種顏色,且相鄰部分的花不同色,則不同的栽種方法共有
某城市在中心廣場建造一個花圃(如圖),花圃分為5個部分,現要將4種顏色的花全部種在花圃中,每部分種一種顏色,且相鄰部分的花不同色,則不同的栽種方法共有查看答案和解析>>
科目:高中數學 來源: 題型:

圖1
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com