
【題目】設函數![]() ,若曲線
,若曲線![]() 上存在
上存在![]() ,使得
,使得![]() 成立,則實數
成立,則實數![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵1cosx1,
∴當cosx=1時, ![]() 取得最小值
取得最小值![]() ,
,
當cosx=1時, ![]() 取得最大值
取得最大值![]() ,
,
即函數![]() 的取值范圍為[1,e],
的取值范圍為[1,e],
若![]() 上存在點(x0,y0)使得f(f(y0))=y0成立,
上存在點(x0,y0)使得f(f(y0))=y0成立,
則y0∈[1,e].且f(y0)=y0.
若下面證明f(y0)=y0.
假設f(y0)=c>y0,則f(f(y0))=f(c)>f(y0)=c>y0,不滿足f(f(y0))=y0.
同理假設f(y0)=c<y0,則不滿足f(f(y0))=y0.
綜上可得:f(y0)=y0.y0∈[1,e].
∵函數![]() 的定義域為(0,+∞),
的定義域為(0,+∞),
∴等價為![]() ,在(0,e]上有解
,在(0,e]上有解
即平方得lnx+x+m=x2,
則a=x2lnxx,
設h(x)=x2lnxx,則![]()
由h′(x)>0得1<x<e,此時函數單調遞增,
由h′(x)<0得0<x<1,此時函數單調遞減,
即當x=1時,函數取得極小值,即h(1)=1ln11=0,
當x=e時,h(e)=e2lnee=e2e1,
則0h(x)e2e1.
則0me2e1.
本題選擇D選項.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】下列命題中__________為真命題(把所有真命題的序號都填上).
①“![]() ”成立的必要條件是“
”成立的必要條件是“![]() ”;
”;
②“若![]() 成等差數列,則
成等差數列,則![]() ”的否命題;
”的否命題;
③“已知數列![]() 的前
的前![]() 項和為
項和為![]() ,若數列
,若數列![]() 是等比數列,則
是等比數列,則![]() 成等比數列.”的逆否命題;
成等比數列.”的逆否命題;
④“已知![]() 是
是![]() 上的單調函數,若
上的單調函數,若![]() ,則
,則![]() ”的逆命題.
”的逆命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn滿足2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差數列.
(1)求a1的值;
(2)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,點A(1,1),B(0,﹣2),C(4,2),D為AB的中點,DE∥BC. (Ⅰ)求BC邊上的高所在直線的方程;
(Ⅱ)求DE所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】教育學家分析發現加強語文樂隊理解訓練與提高數學應用題得分率有關,某校興趣小組為了驗證這個結論,從該校選擇甲乙兩個同軌班級進行試驗,其中甲班加強閱讀理解訓練,乙班常規教學無額外訓練,一段時間后進行數學應用題測試,統計數據情況如下面的![]() 列聯表(單位:人)
列聯表(單位:人)

(1)能夠據此判斷有97.5%把握熱內加強語文閱讀訓練與提高數學應用題得分率有關?
(2)經過多次測試后,小明正確解答一道數學應用題所用的時間在5—7分鐘,小剛正確解得一道數學應用題所用的時間在6—8分鐘,現小明、小剛同時獨立解答同一道數學應用題,求小剛比小明現正確解答完的概率;
(3)現從乙班成績優秀的8名同學中任意抽取兩人,并對他們點答題情況進行全程研究,記A、B兩人中被抽到的人數為X,求X的分布列及數學期望E(X).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一某班的一次數學測試成績(滿分為100分)的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如圖,據此解答如下問題; 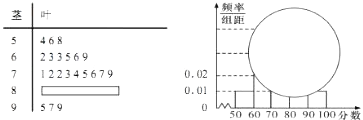
(1)求分數在[50,60)的頻率及全班的人數;
(2)求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(3)根據頻率分布直方圖,估計該班數學成績的平均數與中位數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com