
 中,
中, 底面
底面 ,四邊形
,四邊形 中,
中,  ,
, ,
,  ,
, ,E為
,E為 中點.
中點.
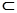 面ABCD ∴PA⊥CD 2分
面ABCD ∴PA⊥CD 2分 ,
, ,且 AB=BC=2
,且 AB=BC=2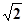 ,∠CAD=45°
,∠CAD=45°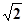
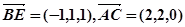 4分
4分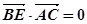
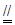 2BC,AG=GD
2BC,AG=GD 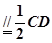
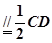
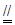 BO ∴BE
BO ∴BE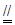 FO
FO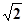 ,BC=2,PC=
,BC=2,PC=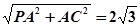 ∴PB⊥BC
∴PB⊥BC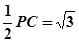
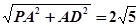 ∴AF=
∴AF=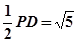
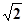 ,OF=BE=
,OF=BE=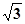 ,AF=
,AF=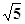 ∴∠AOF=90° 即BE與AC所成的角為90°
∴∠AOF=90° 即BE與AC所成的角為90°

科目:高中數學 來源:不詳 題型:單選題
A.若a α,b α,b α,c⊥a, c⊥b 則c⊥α α,c⊥a, c⊥b 則c⊥α | B.若b α, a//b則 a//α α, a//b則 a//α |
| C.若a//α,α∩β=b則a//b | D.若a⊥α, b⊥α 則a//b |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
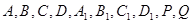 ;(2分)
;(2分)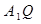 、
、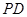 所成角為
所成角為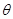 ,求
,求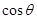 .(6分)
.(6分)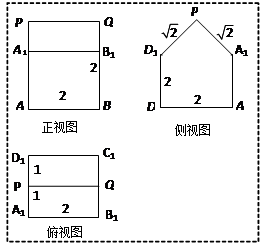
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com